
【题目】如图,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 为
为![]() 中点.
中点.
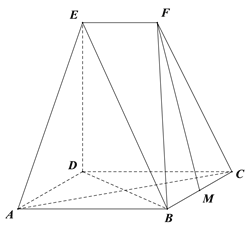
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求证: ![]() ;
;
(3)若![]() 为线段
为线段![]() 上的点,当三棱锥
上的点,当三棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)设![]() ,由三角形中位线性质以及平行四边形性质得四边形
,由三角形中位线性质以及平行四边形性质得四边形![]() 为平行四边形,即得
为平行四边形,即得![]() ∥
∥![]() .再根据线面平行判定定理得结论,(2)根据菱形性质得
.再根据线面平行判定定理得结论,(2)根据菱形性质得![]() ,再根据线面垂直得
,再根据线面垂直得![]() .由线面垂直判定定理得
.由线面垂直判定定理得![]() 平面
平面![]() ,即得结论,(3)过
,即得结论,(3)过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() ,根据条件可得
,根据条件可得![]() 为三棱锥
为三棱锥![]() 的高,再根据三棱锥体积公式列方程解得
的高,再根据三棱锥体积公式列方程解得![]() 的值.
的值.
试题解析:
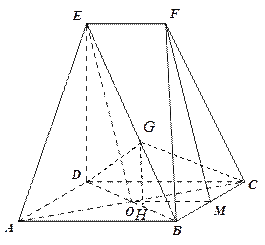
(1) 设![]() ,连结
,连结![]() .
.
因为![]() 分别是
分别是![]() 的中点,
的中点,
因为![]() //
// ![]() ,且
,且![]() ,
,
因为![]() //
// ![]() ,且
,且![]() ,所以
,所以![]() //
// ![]() ,且
,且![]() .
.
所以四边形![]() 为平行四边形.所以
为平行四边形.所以![]() ∥
∥![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平南
平南![]() ,
,
所以![]() ∥平面
∥平面![]() .
.
(2)因为![]() 为菱形,所以
为菱形,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(3)过![]() 作
作![]() 的平行线交
的平行线交![]() 于
于![]() .
.
由已知![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() 为三棱锥
为三棱锥![]() 的高.
的高.
因为三棱锥![]() 的体积为
的体积为![]() ,所以三棱锥
,所以三棱锥![]() 的体积
的体积
![]() .
.
所以![]() .所以
.所以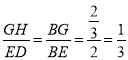 .所以
.所以![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为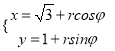 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用极坐标与直角坐标的互化公式可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
,消去参数![]() 可知曲线
可知曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,由直线
的圆,由直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得: ![]() ;则曲线C的方程为
;则曲线C的方程为![]() , 再次利用极坐标与直角坐标的互化公式可得
, 再次利用极坐标与直角坐标的互化公式可得
可得曲线C的极坐标方程.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,
![]() ,
,
由此可求![]() 面积的最大值.
面积的最大值.
试题解析:(1)由题意可知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,直线
的圆,直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得:  ;可知曲线C的方程为
;可知曲线C的方程为![]() ,
,
所以曲线C的极坐标方程为![]() ,
,
即![]() .
.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,

![]() ,
,
当![]() 时,
时, ![]() ,
,
所以△MON面积的最大值为![]() .
.
【题型】解答题
【结束】
23
【题目】已知函数![]() 的定义域为
的定义域为![]() ;
;
(1)求实数![]() 的取值范围;
的取值范围;
(2)设实数![]() 为
为![]() 的最大值,若实数
的最大值,若实数![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有学生500人,学校为了解学生课外阅读时间,从中随机抽取了50名学生,收集了他们2018年10月课外阅读时间(单位:小时)的数据,并将数据进行整理,分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],得到如图所示的频率分布直方图.
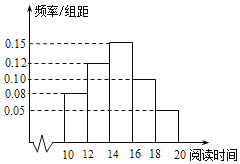
(Ⅰ)试估计该校所有学生中,2018年10月课外阅读时间不小于16小时的学生人数;
(Ⅱ)已知这50名学生中恰有2名女生的课外阅读时间在[18,20],现从课外阅读时间在[18,20]的样本对应的学生中随机抽取2人,求至少抽到1名女生的概率;
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,试估计该校学生2018年10月课外阅读时间的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求经过直线3x+4y-2=0与直线x-y+4=0的交点P,且垂直于直线x-2y-1=0的直线方程;
(2)求过点P(-1,3),并且在两坐标轴上的截距相等的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了配合新冠疫情防控,某市组织了以“停课不停学,成长不停歇”为主题的“空中课堂”,为了了解一周内学生的线上学习情况,从该市中抽取1000名学生进行调査,根据所得信息制作了如图所示的频率分布直方图.
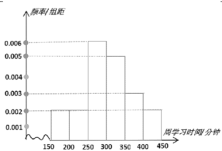
(1)为了估计从该市任意抽取的3名同学中恰有2人线上学习时间在[200,300)的概率![]() ,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示线上学习时间在[200,300)的同学,剩余的数字表示线上学习时间不在[200,300)的同学;再以每三个随机数为一组,代表线上学习的情况.
,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示线上学习时间在[200,300)的同学,剩余的数字表示线上学习时间不在[200,300)的同学;再以每三个随机数为一组,代表线上学习的情况.
假设用上述随机模拟方法已产生了表中的30组随机数,请根据这批随机数估计概率![]() 的值;
的值;
907 966 191 925 271 569 812 458 932 683 431 257 027 556
438 873 730 113 669 206 232 433 474 537 679 138 602 231
(2)为了进一步进行调查,用分层抽样的方法从这1000名学生中抽出20名同学,在抽取的20人中,再从线上学习时间[350,450)(350分钟至450分钟之间)的同学中任意选择两名,求这两名同学来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知![]() =(cosx+sinx,sinx),
=(cosx+sinx,sinx),![]() =(cosx-sinx,2cosx),
=(cosx-sinx,2cosx),
(Ⅰ)求证:向量![]() 与向量
与向量![]() 不可能平行;(Ⅱ)若f(x)=
不可能平行;(Ⅱ)若f(x)=![]() ·,且x∈
·,且x∈![]() 时,求函数f(x)的最大值及最小值
时,求函数f(x)的最大值及最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国著名数学家狄利克雷在数学领域成就显著,以其命名的函数 被称为狄利克雷函数,其中R为实数集,Q为有理数集,以下命题正确的个数是( )
被称为狄利克雷函数,其中R为实数集,Q为有理数集,以下命题正确的个数是( )
下面给出关于狄利克雷函数f(x)的五个结论:
①对于任意的x∈R,都有f(f(x))=1;
②函数f(x)偶函数;
③函数f(x)的值域是{0,1};
④若T≠0且T为有理数,则f(x+T)=f(x)对任意的x∈R恒成立;
⑤在f(x)图象上存在不同的三个点A,B,C,使得△ABC为等边角形.
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com