
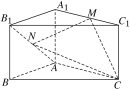
【题目】如图,在直三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=2,点M为A1C1的中点,点N为AB1上一动点.若点N为AB1的中点且CM⊥MN,求二面角MCNA的正弦值.
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:
个税税额=应纳税所得额×税率-速算扣除数.
应纳税所得额的计算公式为:
应纳税所得额=综合所得收入额-免征额-专项扣除-专项附加扣除-依法确定的其他扣除.
其中免征额为每年60000元,税率与速算扣除数见下表:
级数 | 全年应纳税所得额所在区间 | 税率( | 速算扣除数 |
1 |
| 3 | 0 |
2 |
| 10 | 2520 |
3 |
| 20 | 16920 |
4 |
| 25 | 31920 |
5 |
| 30 | 52920 |
6 |
| 35 | 85920 |
7 |
| 45 | 181920 |
备注:
“专项扣除”包括基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金。
“专项附加扣除”包括子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等支出。
“其他扣除”是指除上述免征额、专项扣除、专项附加扣除之外,由国务院决定以扣除方式减少纳税的优惠政策规定的费用。
某人全年综合所得收入额为160000元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是![]() ,
,![]() ,
,![]() ,
,![]() ,专项附加扣除是24000元,依法确定其他扣除是0元,那么他全年应缴纳综合所得个税____元.
,专项附加扣除是24000元,依法确定其他扣除是0元,那么他全年应缴纳综合所得个税____元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点为
的左右焦点为![]() 为它的中心,
为它的中心,![]() 为双曲线右支上的一点,
为双曲线右支上的一点,![]() 的内切圆圆心为
的内切圆圆心为![]() ,且圆
,且圆![]() 与
与![]() 轴相切于
轴相切于![]() 点,过
点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若双曲线的离心率为
,若双曲线的离心率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 与
与![]() 关系不确定
关系不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
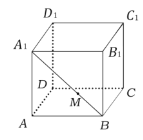
【题目】如图,棱长为1的正方体![]() 中,
中,![]() 是线段
是线段![]() 上的动点,则下列结论正确的是( ).
上的动点,则下列结论正确的是( ).
①异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
②![]()
③三棱锥![]() 的体积为定值
的体积为定值
④![]() 的最小值为2.
的最小值为2.
A.①②③B.①②④C.③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过焦点且垂直于
,过焦点且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 所截得的弦长为
所截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 是坐标原点,求
是坐标原点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合![]() 是由一些函数组成,满足如下性质:①对任意
是由一些函数组成,满足如下性质:①对任意![]() ,
,![]() 均存在反函数
均存在反函数![]() ,且
,且![]() ;②对任意
;②对任意![]() ,方程
,方程![]() 均有解;③对任意
均有解;③对任意![]() 、
、![]() ,若函数
,若函数![]() 为定义在
为定义在![]() 上的一次函数,则
上的一次函数,则![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求证:函数
中,求证:函数![]() ;
;
(2)若函数![]() (
(![]() )在集合
)在集合![]() 中,求实数
中,求实数![]() 的取值范围;
的取值范围;
(3)若集合![]() 中的函数均为定义在
中的函数均为定义在![]() 上的一次函数,求证:存在一个实数
上的一次函数,求证:存在一个实数![]() ,使得对一切
,使得对一切![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大湖名城,创新高地”的合肥,历史文化积淀深厚,民俗和人文景观丰富,科教资源众多,自然风光秀美,成为中小学生“研学游”的理想之地.为了将来更好地推进“研学游”项目,某旅游学校一位实习生,在某旅行社实习期间,把“研学游”项目分为科技体验游、民俗人文游、自然风光游三种类型,并在前几年该旅行社接待的全省高一学生“研学游”学校中,随机抽取了100所学校,统计如下:
研学游类型 | 科技体验游 | 民俗人文游 | 自然风光游 |
学校数 | 40 | 40 | 20 |
该实习生在明年省内有意向组织高一“研学游”学校中,随机抽取了3所学校,并以统计的频率代替学校选择研学游类型的概率(假设每所学校在选择研学游类型时仅选择其中一类,且不受其他学校选择结果的影响):
(1)若这3所学校选择的研学游类型是“科技体验游”和“自然风光游”,求这两种类型都有学校选择的概率;
(2)设这3所学校中选择“科技体验游”学校数为随机变量X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 两点分别在函数
两点分别在函数![]() 与
与![]() 的图像上,且关于直线
的图像上,且关于直线![]() 对称,则称
对称,则称![]() 、
、![]() 是
是![]() 与
与![]() 的一对“伴点”(
的一对“伴点”(![]() 、
、![]() 与
与![]() 、
、![]() 视为相同的一对).已知
视为相同的一对).已知 ,
,![]() ,若
,若![]() 与
与![]() 存在两对“伴点”,则实数
存在两对“伴点”,则实数![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com