
【题目】如图,在![]() 中,已知点D在边AB上,AD=3DB,
中,已知点D在边AB上,AD=3DB,
![]() ,
, ![]() ,BC=13.
,BC=13.
(1)求![]() 的值;
的值;
(2)求CD的长.
【答案】(1) ![]() (2)9
(2)9![]()
【解析】试题分析:(1)在△ABC中,求出sinA=![]() ,sin∠ACB=
,sin∠ACB=![]() ,
,
可得cosB=-cos(A+∠ACB)=sinAsin∠ACB-cosAcosB;
(2)在△ABC中,由正弦定理得,AB= ![]() ∠ACB.
∠ACB.
在△BCD中,由余弦定理得,CD=![]() 代入即得解.
代入即得解.
试题解析:
(1)在△ABC中, cosA=![]() ,A
,A![]() ,
,
所以 sinA=![]() .
.
同理可得sin∠ACB=![]() .
.
所以cosB=-cos(![]() –(A+∠ACB))= -cos(A+∠ACB)=sinAsin∠ACB-cosAcosB=
–(A+∠ACB))= -cos(A+∠ACB)=sinAsin∠ACB-cosAcosB=![]() .
.
(2)在△ABC中,由正弦定理得, AB= ![]() ∠ACB =
∠ACB =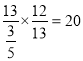 .
.
又AD=3DB,所以 ![]()
又在△BCD 中,由余弦定理得,
CD=![]()


科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,
(1)请补全函数f(x)的图象 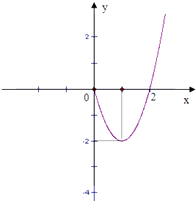
(2)求函数f(x)的表达式,
(3)写出函数f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为 ![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点P(0,2),l和C交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学得到方程2x+e﹣0.3x﹣100=0(其中e=2.7182…)的大于零的近似解依次为①50;②50.1;③49.5;④50.001,你认为的答案为最佳近似解(请填甲、乙、丙、丁中的一个)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当a>0时,求函数f(x)的单调递减区间;
(Ⅱ)当a=0时,设函数g(x)=xf(x)﹣k(x+2)+2.若函数g(x)在区间![]() 上有两个零点,求实数k的取值范围.
上有两个零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海南中学对高二学生进行心理障碍测试得到如下列联表:
焦虑 | 说谎 | 懒惰 | 总计 | |
女生 | 5 | 10 | 15 | 30 |
男生 | 20 | 10 | 50 | 80 |
总计 | 25 | 20 | 65 | 110 |
试说明在这三种心理障碍中哪一种与性别关系最大?
参考数据:K2= ![]()
P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com