
| A. | $\left\{{\begin{array}{l}{x={t^2}}\\{y={t^4}}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=sint}\\{y={{sin}^2}t}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=t}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=t}\\{y={t^2}}\end{array}}\right.$ |
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:填空题
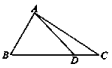
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
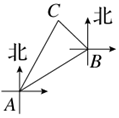 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A出出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.| A. | 5($\sqrt{6}$+$\sqrt{2}$) | B. | 5($\sqrt{6}$-$\sqrt{2}$) | C. | 10($\sqrt{6}$+$\sqrt{2}$) | D. | 10($\sqrt{6}$-$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com