
【题目】已知两个定点![]() ,
,![]() , 动点
, 动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() :
:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线QM、QN,切点为
的两条切线QM、QN,切点为![]() 、
、![]() ,探究:直线
,探究:直线![]() 是否过定点,若存在定点请写出坐标,若不存在则说明理由.
是否过定点,若存在定点请写出坐标,若不存在则说明理由.
科目:高中数学 来源: 题型:
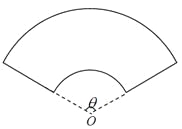
【题目】某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 是我国古代著名数学经典
是我国古代著名数学经典![]() 其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小
其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小![]() 以锯锯之,深一寸,锯道长一尺
以锯锯之,深一寸,锯道长一尺![]() 问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺
问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺![]() 问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示
问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示![]() 阴影部分为镶嵌在墙体内的部分
阴影部分为镶嵌在墙体内的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈
寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列结论:
①函数y=2x的图象与函数y=log2x的图象关于y轴对称;
②函数y=ax+2(a>0且a≠1)的图象可以由函数y=ax的图象平移得到;
③方程log5(2x+1)=log5(x2-2)的解集为{-1,3};
④函数y=ln(1+x)-ln(1-x)为奇函数.
其中不正确的是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)若集合A={x|x2+5x﹣6=0},B={x|x2+2(m+1)x+m2﹣3=0}.
(1)若m=0,写出A∪B的子集;
(2)若A∩B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x≥0时,f(x)=![]() .
.
(1)求f(x)的解析式;
(2)判断f(x)的单调性;
(3)若对任意的t∈R,不等式f(k-3t2)+f(t2+2t)≤0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:
①函数y=cos(-2x)的最小正周期是π;
②终边在y轴上的角的集合是{α|α=![]() ,k∈Z};
,k∈Z};
③在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④函数y=sin(x-![]() )在[0,π]上是增函数.其中,正确的说法是________.(填序号)
)在[0,π]上是增函数.其中,正确的说法是________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com