
ΓΨΧβΡΩΓΩΚ· ΐfnΘ®xΘ©=xn+bx+cΘ®nΓ ZΘ§bΘ§cΓ RΘ©Θ°
Θ®1Θ©»τn=©¹1Θ§«“f©¹1Θ®1Θ©=f©¹1Θ® ![]() Θ©=4Θ§ ‘«σ Β ΐbΘ§cΒΡ÷ΒΘΜ
Θ©=4Θ§ ‘«σ Β ΐbΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©…ηn=2Θ§»τΕ‘»Έ“βx1 Θ§ x2Γ [©¹1Θ§1]”–|f2Θ®x1Θ©©¹f2Θ®x2Θ©|Γή4Κψ≥…ΝΔΘ§«σbΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©Β±n=1 ±Θ§“―÷Σbx2+cx©¹a=0Θ§…ηgΘ®xΘ©= ![]() Θ§ «Ζώ¥φ‘Ύ’ΐ ΐaΘ§ ΙΒΟΕ‘”Ύ«χΦδ
Θ§ «Ζώ¥φ‘Ύ’ΐ ΐaΘ§ ΙΒΟΕ‘”Ύ«χΦδ ![]() …œΒΡ»Έ“β»ΐΗω Β ΐmΘ§nΘ§pΘ§ΕΦ¥φ‘Ύ“‘f1Θ®gΘ®mΘ©Θ©Θ§f1Θ®gΘ®nΘ©Θ©Θ§f1Θ®gΘ®pΘ©Θ©ΈΣ±Ώ≥ΛΒΡ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωaΒΡ»Γ÷ΒΖΕΈßΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
…œΒΡ»Έ“β»ΐΗω Β ΐmΘ§nΘ§pΘ§ΕΦ¥φ‘Ύ“‘f1Θ®gΘ®mΘ©Θ©Θ§f1Θ®gΘ®nΘ©Θ©Θ§f1Θ®gΘ®pΘ©Θ©ΈΣ±Ώ≥ΛΒΡ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«σ≥ωaΒΡ»Γ÷ΒΖΕΈßΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚn=©¹1Θ§«“ ![]() Θ§
Θ§
Ω…ΒΟ1+b+c=4Θ§2+ ![]() b+c=4Θ§ΫβΒΟb=2Θ§c=1ΘΜ
b+c=4Θ§ΫβΒΟb=2Θ§c=1ΘΜ
Θ®2Θ©ΫβΘΚΒ±n=2 ±Θ§f2Θ®xΘ©=x2+bx+cΘ§
Ε‘»Έ“βx1Θ§x2Γ [©¹1Θ§1]”–|f2Θ®x1Θ©©¹f2Θ®x2Θ©|Γή4Κψ≥…ΝΔΒ»Φέ”Ύ
f2Θ®xΘ©‘Ύ[©¹1Θ§1]…œΒΡΉν¥σ÷Β”κΉν–Γ÷Β÷°≤νMΓή4Θ°
ΔΌΒ±©¹ ![]() ΘΦ©¹1Θ§Φ¥bΘΨ2 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§1]Βί‘ωΘ§
ΘΦ©¹1Θ§Φ¥bΘΨ2 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§1]Βί‘ωΘ§
f2Θ®xΘ©min=f2Θ®©¹1Θ©=1©¹b+cΘ§f2Θ®xΘ©max=f2Θ®1Θ©=1+b+cΘ§
M=2bΘΨ4Θ®…α»ΞΘ©ΘΜ
ΔΎΒ±©¹1Γή©¹ ![]() Γή0Θ§Φ¥0ΓήbΓή2 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§©¹
Γή0Θ§Φ¥0ΓήbΓή2 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§©¹ ![]() ]ΒίΦθΘ§‘ΎΘ®©¹
]ΒίΦθΘ§‘ΎΘ®©¹ ![]() Θ§1]Βί‘ωΘ§
Θ§1]Βί‘ωΘ§
f2Θ®xΘ©min=f2Θ®©¹ ![]() Θ©=c©¹
Θ©=c©¹ ![]() Θ§f2Θ®xΘ©max=f2Θ®1Θ©=1+b+cΘ§M=Θ®
Θ§f2Θ®xΘ©max=f2Θ®1Θ©=1+b+cΘ§M=Θ® ![]() +1Θ©2Γή4Κψ≥…ΝΔΘ§Ι 0ΓήbΓή2ΘΜ
+1Θ©2Γή4Κψ≥…ΝΔΘ§Ι 0ΓήbΓή2ΘΜ
ΔέΒ±0ΘΦ©¹ ![]() Γή1Φ¥©¹2ΓήbΘΦ0 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§©¹
Γή1Φ¥©¹2ΓήbΘΦ0 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§©¹ ![]() ]ΒίΦθΘ§‘ΎΘ®©¹
]ΒίΦθΘ§‘ΎΘ®©¹ ![]() Θ§1]Βί‘ωΘ§
Θ§1]Βί‘ωΘ§
f2Θ®xΘ©min=f2Θ®©¹ ![]() Θ©=c©¹
Θ©=c©¹ ![]() Θ§f2Θ®xΘ©max=f2Θ®©¹1Θ©=1©¹b+cΘ§M=Θ®
Θ§f2Θ®xΘ©max=f2Θ®©¹1Θ©=1©¹b+cΘ§M=Θ® ![]() ©¹1Θ©2Γή4Κψ≥…ΝΔΘ§Ι ©¹2ΓήbΘΦ0ΘΜ
©¹1Θ©2Γή4Κψ≥…ΝΔΘ§Ι ©¹2ΓήbΘΦ0ΘΜ
ΔήΒ±©¹ ![]() ΘΨ1Θ§Φ¥bΘΦ©¹2 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§1]ΒίΦθΘ§
ΘΨ1Θ§Φ¥bΘΦ©¹2 ±Θ§f2Θ®xΘ©‘Ύ[©¹1Θ§1]ΒίΦθΘ§
f2Θ®xΘ©min=f2Θ®1Θ©=1+b+cΘ§f2Θ®xΘ©max=f2Θ®©¹1Θ©=1©¹b+cΘ§
M=©¹2bΘΨ4Ο§ΕήΘ°
Ήέ…œΩ…ΒΟΘ§bΒΡ»Γ÷ΒΖΕΈß «©¹2ΓήbΓή2ΘΜ
Θ®3Θ©ΫβΘΚ…ηt=gΘ®xΘ©= ![]() =
= ![]() =
= ![]() Θ§
Θ§
”…xΓ 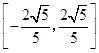 Θ§Ω…ΒΟtΓ [
Θ§Ω…ΒΟtΓ [ ![]() Θ§1]Θ°
Θ§1]Θ°
‘ρy=t+ ![]() ‘Ύ[
‘Ύ[ ![]() Θ§1]…œΚψ”–2yminΘΨymaxΘ°
Θ§1]…œΚψ”–2yminΘΨymaxΘ°
ΔΌΒ±aΓ Θ®0Θ§ ![]() ] ±Θ§y=t+
] ±Θ§y=t+ ![]() ‘Ύ[
‘Ύ[ ![]() Θ§1]…œΒί‘ωΘ§
Θ§1]…œΒί‘ωΘ§
ymin= ![]() +3aΘ§ymax=a+1Θ§”÷2yminΘΨymaxΘ°
+3aΘ§ymax=a+1Θ§”÷2yminΘΨymaxΘ°
‘ρaΘΨ ![]() Θ§Φ¥”–
Θ§Φ¥”– ![]() ΘΦaΓή
ΘΦaΓή ![]() ΘΜ
ΘΜ
ΔΎΒ±aΓ Θ® ![]() Θ§
Θ§ ![]() ] ±Θ§y=t+
] ±Θ§y=t+ ![]() ‘Ύ[
‘Ύ[ ![]() Θ§
Θ§ ![]() Θ©ΒίΦθΘ§Θ®
Θ©ΒίΦθΘ§Θ® ![]() Θ§1Θ©Βί‘ωΘ§
Θ§1Θ©Βί‘ωΘ§
Ω…ΒΟymin=2 ![]() Θ§ymax=max{3a+
Θ§ymax=max{3a+ ![]() Θ§a+1}=a+1Θ§”÷2yminΘΨymaxΘ°
Θ§a+1}=a+1Θ§”÷2yminΘΨymaxΘ°
ΫβΒΟ7©¹4 ![]() ΘΦaΘΦ7+4
ΘΦaΘΦ7+4 ![]() Θ§Φ¥”–
Θ§Φ¥”– ![]() ΘΦaΓή
ΘΦaΓή ![]() ΘΜ
ΘΜ
ΔέΒ±aΓ Θ® ![]() Θ§1Θ© ±Θ§y=t+
Θ§1Θ© ±Θ§y=t+ ![]() ‘Ύ[
‘Ύ[ ![]() Θ§
Θ§ ![]() Θ©ΒίΦθΘ§Θ®
Θ©ΒίΦθΘ§Θ® ![]() Θ§1Θ©Βί‘ωΘ§
Θ§1Θ©Βί‘ωΘ§
Ω…ΒΟymin=2 ![]() Θ§ymax=max{3a+
Θ§ymax=max{3a+ ![]() Θ§a+1}=3a+
Θ§a+1}=3a+ ![]() Θ§”÷2yminΘΨymaxΘ°
Θ§”÷2yminΘΨymaxΘ°
ΫβΒΟ ![]() ΘΦaΘΦ
ΘΦaΘΦ ![]() Θ§Φ¥”–
Θ§Φ¥”– ![]() ΘΦaΘΦ1ΘΜ
ΘΦaΘΦ1ΘΜ
ΔήΒ±aΓ [1Θ§+ΓόΘ© ±Θ§y=t+ ![]() ‘Ύ[
‘Ύ[ ![]() Θ§1]…œΒίΦθΘ§
Θ§1]…œΒίΦθΘ§
ymin=a+1Θ§ymax=3a+ ![]() Θ§”÷2yminΘΨymaxΘ°
Θ§”÷2yminΘΨymaxΘ°
‘ρaΘΦ ![]() Θ§Φ¥”–1ΓήaΘΦ
Θ§Φ¥”–1ΓήaΘΦ ![]() Θ°
Θ°
Ήέ…œΩ…ΒΟΘ§¥φ‘Ύ’β―υΒΡ»ΐΫ«–ΈΘ§aΒΡ»Γ÷ΒΖΕΈß « ![]() ΘΦaΘΦ
ΘΦaΘΦ ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©”…ΧθΦΰΘ§Ω…ΒΟbΘ§cΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΩ…ΒΟbΘ§cΘΜΘ®2Θ©Β±n=2 ±Θ§f2Θ®xΘ©=x2+bx+cΘ§Ε‘»Έ“βx1Θ§x2Γ [©¹1Θ§1]”–|f2Θ®x1Θ©©¹f2Θ®x2Θ©|Γή4Κψ≥…ΝΔΒ»Φέ”Ύf2Θ®xΘ©‘Ύ[©¹1Θ§1]…œΒΡΉν¥σ÷Β”κΉν–Γ÷Β÷°≤νMΓή4Θ°Χ÷¬έΕ‘≥Τ÷αΚΆ«χΦδΒΡΙΊœΒΘ§≈–ΕœΒΞΒς–‘Θ§Ω…ΒΟΉν÷ΒΘ§Ϋβ≤ΜΒ» ΫΦ¥Ω…ΒΟΒΫΥυ«σΖΕΈßΘΜΘ®3Θ©…ηt=gΘ®xΘ©= ![]() =
= ![]() =
= ![]() Θ§”…xΓ
Θ§”…xΓ ![]() Θ§Ω…ΒΟtΓ [
Θ§Ω…ΒΟtΓ [ ![]() Θ§1]Θ°‘ρy=t+
Θ§1]Θ°‘ρy=t+ ![]() ‘Ύ[
‘Ύ[ ![]() Θ§1]…œΚψ”–2yminΘΨymaxΘ°Χ÷¬έΕΞΒψ¥Πx=
Θ§1]…œΚψ”–2yminΘΨymaxΘ°Χ÷¬έΕΞΒψ¥Πx= ![]() ”κ«χΦδ[
”κ«χΦδ[ ![]() Θ§1]ΒΡΙΊœΒΘ§«σΒΟΒΞΒς–‘Θ§Ω…ΒΟΉν÷ΒΘ§Ϋβ≤ΜΒ» ΫΦ¥Ω…ΒΟΒΫ¥φ‘ΎΘ§«σΒΟaΒΡΖΕΈßΘ°
Θ§1]ΒΡΙΊœΒΘ§«σΒΟΒΞΒς–‘Θ§Ω…ΒΟΉν÷ΒΘ§Ϋβ≤ΜΒ» ΫΦ¥Ω…ΒΟΒΫ¥φ‘ΎΘ§«σΒΟaΒΡΖΕΈßΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΥ“ΚΘ¬÷¥”A≥ωΖΔΘ§―Ί±±ΤΪΕΪ75ΓψΒΡΖΫœρΚΫ––Θ®2 ![]() ©¹2Θ©nmileΒΫ¥οΚΘΒΚBΘ§»ΜΚσ¥”B≥ωΖΔΘ§―Ί±±ΤΪΕΪ15ΓψΒΡΖΫœρΚΫ––4nmileΒΫ¥οΚΘΒΚCΘ°
©¹2Θ©nmileΒΫ¥οΚΘΒΚBΘ§»ΜΚσ¥”B≥ωΖΔΘ§―Ί±±ΤΪΕΪ15ΓψΒΡΖΫœρΚΫ––4nmileΒΫ¥οΚΘΒΚCΘ° 
Θ®1Θ©«σACΒΡ≥ΛΘΜ
Θ®2Θ©»γΙϊœ¬¥ΈΚΫ––÷±Ϋ”¥”A≥ωΖΔΒΫ¥οCΘ§«σΓœCABΒΡ¥σ–ΓΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γœ¬ΆΦΘ§÷±»ΐάβ÷υABCΘ≠A1B1C1ΒΡΒΉΟφ «±Ώ≥ΛΈΣ2ΒΡ’ΐ»ΐΫ«–ΈΘ§EΓΔFΖ÷±π «BCΓΔCC1ΒΡ÷–Βψ.
Θ®1Θ©÷ΛΟςΘΚΤΫΟφAEFΓΆΤΫΟφB1BCC1ΘΜ
Θ®2Θ©»τ÷±œΏA1C”κΤΫΟφA1ABB1Υυ≥…ΒΡΫ«ΈΣ45ΓψΘ§«σ»ΐάβΉΕFΘ≠AECΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σan=logn+1Θ®n+2Θ©Θ®nΓ N+Θ©Θ§Ιέ≤λœ¬Ν–‘ΥΥψΘΚa1a2=log23log34= ![]() =2ΘΜa1a2a3a4a5a6=log23log34Γ≠log67lg78=
=2ΘΜa1a2a3a4a5a6=log23log34Γ≠log67lg78= ![]() =3ΘΜΓ≠Θ°Ε®“ε Ιa1a2a3Γ≠akΈΣ’ϊ ΐΒΡkΘ®kΓ N+Θ©Ϋ–ΉωœΘΆϊ ΐΘ§‘ρ‘Ύ«χΦδ[1Θ§2016]ΡΎΥυ”–œΘΆϊ ΐΒΡΚΆΈΣΘ® Θ©
=3ΘΜΓ≠Θ°Ε®“ε Ιa1a2a3Γ≠akΈΣ’ϊ ΐΒΡkΘ®kΓ N+Θ©Ϋ–ΉωœΘΆϊ ΐΘ§‘ρ‘Ύ«χΦδ[1Θ§2016]ΡΎΥυ”–œΘΆϊ ΐΒΡΚΆΈΣΘ® Θ©
A.1004
B.2026
C.4072
D.22016©¹2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–{an}ΈΣΒΞΒςΒίΦθΒΡΒ»≤ν ΐΝ–Θ§a1+a2+a3=21Θ§«“a1©¹1Θ§a2©¹3Θ§a3©¹3≥…Β»±» ΐΝ–Θ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…ηbn=|an|Θ§«σ ΐΝ–{bn}ΒΡ«ΑœνnΚΆTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§«“
Θ§«“![]() .
.
Θ®1Θ©«σ ΐΝ–![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…η![]() Θ§«σ ΐΝ–
Θ§«σ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆ
œνΚΆ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣfΘ®xΘ©ΈΣΕ®“ε‘Ύ[©¹1Θ§1]…œΒΡΤφΚ· ΐΘ§Β±xΓ [©¹1Θ§0] ±Θ§Κ· ΐΫβΈω ΫΈΣ ![]() Θ° Θ®ΔώΘ©«σfΘ®xΘ©‘Ύ[0Θ§1]…œΒΡΫβΈω ΫΘΜ
Θ° Θ®ΔώΘ©«σfΘ®xΘ©‘Ύ[0Θ§1]…œΒΡΫβΈω ΫΘΜ
Θ®ΔρΘ©«σfΘ®xΘ©‘Ύ[0Θ§1]…œΒΡΉν÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–Θ100Οϊ―ß…ζΤΎ÷–ΩΦ ‘”οΈΡ≥…Φ®ΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γΆΦΥυ ΨΘ§Τδ÷–≥…Φ®Ζ÷Ήι«χΦδ «ΘΚ[50Θ§60Θ©Θ§[60Θ§70Θ©Θ§[70Θ§80Θ©Θ§[80Θ§90Θ©Θ§[90Θ§100]Θ° 
Θ®1Θ©«σΆΦ÷–aΒΡ÷ΒΘΜ
Θ®2Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΙάΦΤ’β100Οϊ―ß…ζ”οΈΡ≥…Φ®ΒΡΤΫΨυΖ÷ΘΜ
Θ®3Θ©»τ’β100Οϊ―ß…ζ”οΈΡ≥…Φ®Ρ≥–©Ζ÷ ΐΕΈΒΡ»Υ ΐΘ®xΘ©”κ ΐ―ß≥…Φ®œύ”ΠΖ÷ ΐΕΈΒΡ»Υ ΐΘ®yΘ©÷°±»»γ±μΥυ ΨΘ§«σ ΐ―ß≥…Φ®‘Ύ[50Θ§90Θ©÷°ΆβΒΡ»Υ ΐΘ°
Ζ÷ ΐΕΈ | [50Θ§60Θ© | [60Θ§70Θ© | [70Θ§80Θ© | [80Θ§90Θ© |
xΘΚy | 1ΘΚ1 | 2ΘΚ1 | 3ΘΚ4 | 4ΘΚ5 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤–Ρ‘Ύ÷±œΏx+y©¹1=0…œ«“ΙΐΒψAΘ®2Θ§2Θ©ΒΡ‘≤C1”κ÷±œΏ3x©¹4y+5=0œύ«–Θ§ΤδΑκΨΕ–Γ”Ύ5Θ°
Θ®1Θ©»τC2‘≤”κ‘≤C1ΙΊ”Ύ÷±œΏx©¹y=0Ε‘≥ΤΘ§«σ‘≤C2ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©Ιΐ÷±œΏy=2x©¹6…œ“ΜΒψPΉς‘≤C2ΒΡ«–œΏPCΘ§PDΘ§«–ΒψΈΣCΘ§DΘ§Β±ΥΡ±Ώ–ΈPCC2DΟφΜΐΉν–Γ ±Θ§«σ÷±œΏCDΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com