
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为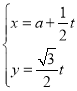 ,以直角坐标系
,以直角坐标系![]() 的
的![]() 点为极点,
点为极点,![]() 为极轴,且取相同的长度单位,建立极坐标系,已知圆
为极轴,且取相同的长度单位,建立极坐标系,已知圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的倾斜角;
的倾斜角;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 的面积最大时,求实数
的面积最大时,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】足不出户,手机下单,送菜到家,轻松逛起手机“菜市场”,拎起手机“菜篮子”.在省时省心的同时,线上买菜也面临着质量不佳、物流滞后等问题.“指尖”上的菜篮子该如何守护“舌尖”上的幸福感?某手机APP(应用程序)公司为了解这款APP使用者的满意度,对一小区居民开展“线上购买食品满意度调查”活动,邀请每位使用者填写一份满意度测评表(满分100分).该公司最后共收回1100份测评表,随机抽取了100份作为样本,得到如下数据:

(1)从表中数据估计,收回的测评表中,评分不小于80分的女性人数;
(2)该公司根据经验,对此APP使用者划分“用户类型”:评分不小于80分的为“A类用户”,评分小于80分的为“B类用户
(i)请根据100个样本数据,完成下面列联表:

(ⅱ)根据列联表判断能否有95%的把握认为“用户类型”与性别有关?
附:K2

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象向右平移一个单位,所得图象与函数
的图象向右平移一个单位,所得图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称;已知偶函数
对称;已知偶函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ;若函数
;若函数![]() 有五个零点,则
有五个零点,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有两种日工资方案供员工选择,方案一规定每日底薪50元,计件工资每件3元;方案二规定每日底薪100元,若生产的产品数不超过44则没有计件工资,若超过则从第45件开始,计件工资每件5元.该工厂随机抽取100天的工人生产量的数据.将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,整理得到如图所示的频率分布直方图.
七组,整理得到如图所示的频率分布直方图.
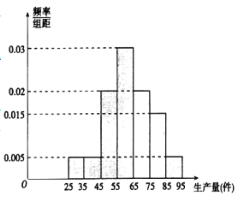
(1)随机选取一天,估计这一天该工厂的人均生产量不少于65件的概率;
(2)若甲、乙选择了日工资方案一,丙、丁选择了日工资方案二.现从上述4名工人中随机选取2人.求至少有1名工人选择方案一的概率;
(3)若仅从人均日收入的角度考虑,请你利用所学的统计学知识为新聘工人做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
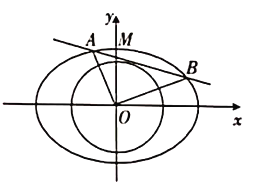
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
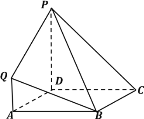
【题目】在如图所示的几何体中,四边形![]() 是正方形,四边形
是正方形,四边形![]() 是梯形,
是梯形,![]() ∥
∥![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)已知点![]() 在棱
在棱![]() 上,且异面直线
上,且异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com