
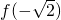 是f(x)的极小值,
是f(x)的极小值,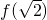 是f(x)的极大值;
是f(x)的极大值; =(1,1),
=(1,1), =(1,-1),则向量
=(1,-1),则向量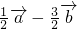 =(-2,-1);
=(-2,-1); ,
, 或x<-
或x<- ,由f′(x)>0得-
,由f′(x)>0得- <x<
<x< ,
, ),(
),( ,+∞),单调增区间为(-
,+∞),单调增区间为(- ,
, );
); ),极小值为f(-
),极小值为f(- ),故(1)正确.
),故(1)正确.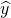 =3-2.5x,①当自变量由x变为x+1时,y=3-2.5(x+1)②,∴②-①得y-
=3-2.5x,①当自变量由x变为x+1时,y=3-2.5(x+1)②,∴②-①得y- =-2.5
=-2.5 =(1,1),
=(1,1), =(1,-1),则向量
=(1,-1),则向量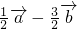 =
=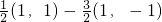 =(-1,2),所以(3)不正确.
=(-1,2),所以(3)不正确. x2,所以y′=x,过点P,Q的抛物线的切线的斜率分别为4,-2,所以过点P,Q的抛物线的切线方程分别为y=4x-8,y=-2x-2 联立方程组解得x=1,y=-4 故点A的纵坐标为-4.所以(4)正确.
x2,所以y′=x,过点P,Q的抛物线的切线的斜率分别为4,-2,所以过点P,Q的抛物线的切线方程分别为y=4x-8,y=-2x-2 联立方程组解得x=1,y=-4 故点A的纵坐标为-4.所以(4)正确. 的结果判断正误即可.
的结果判断正误即可.

科目:高中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com