Question

7．已知函数f（x）=$\frac{2x+b}{x-a}$（x∈R，x≠a）．
（1）若函数f（x）的图象关于直线y=x对称，求实数a的值；
（2）若函数F（x）=$\frac{a}{f（x）}$（a≠0），且F（x）的反函数F^-1（x）的图象如图，求出a、b的值，并写出F^-1（x）的表达式．

Answer 1

分析 （1）由函数f（x）的图象关于直线y=x对称，说明其反函数就是本身，求出其反函数，然后由两个解析式相等求得a值；
（2）由F^-1（x）的图象过（0，6），且对称中心的纵坐标为-2，横坐标大于0，可得函数F（x）的图象过点（6，0），且对称中心的横坐标为-2，纵坐标大于0．
然后把F（x）=$\frac{a}{f（x）}$变形，根据函数图象的平移得到其对称中心的横坐标，结合F（6）=0联立方程组求得a、b的值，则F^-1（x）的表达式可求．

解答 解：（1）由y=f（x）=$\frac{2x+b}{x-a}$，得yx-ay=2x+b，即x=$\frac{ay+b}{y-2}$，∴y=$\frac{ax+b}{x-2}$．
∵函数f（x）的图象关于直线y=x对称，∴$\frac{ax+b}{x-2}$=$\frac{2x+b}{x-a}$，即a=2；
（2）F（x）=$\frac{a}{f（x）}$=$\frac{a}{\frac{2x+b}{x-a}}=\frac{ax-{a}^{2}}{2x+b}$=$\frac{\frac{a}{2}（2x+b）-{a}^{2}-\frac{ab}{2}}{2x+b}$=$\frac{a}{2}-\frac{\frac{2{a}^{2}+ab}{4}}{x+\frac{b}{2}}$，
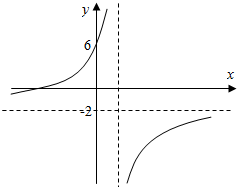
由图可知，函数F^-1（x）的图象过（0，6），且对称中心的纵坐标为-2，横坐标大于0．
∴函数F（x）的图象过点（6，0），且对称中心的横坐标为-2，纵坐标大于0．
∴$\left\{\begin{array}{l}{\frac{6a-{a}^{2}}{12+b}=0}\\{-\frac{b}{2}=-2}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=6}\\{b=4}\end{array}\right.$．
∴F（x）=$\frac{6x-36}{2x+4}=\frac{3x-18}{x+2}$，
由y=$\frac{3x-18}{x+2}$，得x=$\frac{2y+18}{3-y}$，x，y互换得：$y=\frac{2x+18}{3-x}$．
则F^-1（x）=$\frac{2x+18}{3-x}$．

点评 本题考查函数的反函数的求法，考查了函数特性的平移，体现了数学转化思想方法，属中档题．