
【题目】某公司10位员工的月工资(单位:元)为x1 , x2 , …,x10 , 其均值和方差分别为 ![]() 和s2 , 若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
和s2 , 若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
A.![]() ,s2+1002
,s2+1002
B.![]() +100,s2+1002
+100,s2+1002
C.![]() ,s2
,s2
D.![]() +100,s2
+100,s2
【答案】D
【解析】解:由题意知yi=xi+100, 则 ![]() =
= ![]() (x1+x2+…+x10+100×10)=
(x1+x2+…+x10+100×10)= ![]() (x1+x2+…+x10)=
(x1+x2+…+x10)= ![]() +100,
+100,
方差s2= ![]() [(x1+100﹣(
[(x1+100﹣( ![]() +100)2+(x2+100﹣(v+100)2+…+(x10+100﹣(
+100)2+(x2+100﹣(v+100)2+…+(x10+100﹣( ![]() +100)2]=
+100)2]= ![]() [(x1﹣
[(x1﹣ ![]() )2+(x2﹣
)2+(x2﹣ ![]() )2+…+(x10﹣
)2+…+(x10﹣ ![]() )2]=s2 .
)2]=s2 .
故选:D.
【考点精析】解答此题的关键在于理解平均数、中位数、众数的相关知识,掌握⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据,以及对极差、方差与标准差的理解,了解标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=x2-x+15,且|x-a|<1,
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求证:|f(x)-f(a)|<2(|a|+1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a. 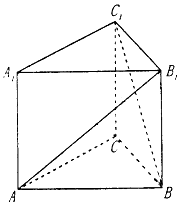
(1)求证:AB1⊥BC1;
(2)求二面角B﹣AB1﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下几个命题中真命题的序号为 .
①在空间中,m、n是两条不重合的直线,α、β是两个不重合的平面,如果α⊥β,α∩β=n,m⊥n,那么m⊥β;
②相关系数r的绝对值越接近于1,两个随机变量的线性相关性越强;
③用秦九昭算法求多项式f(x)=208+9x2+6x4+x6在x=﹣4时,v2的值为22;
④过抛物线y2=4x的焦点作直线与抛物线相交于A、B两点,则使它们的横坐标之和等于4的直线有且只有两条.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com