
【题目】本公司计划2008年在甲,乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲,乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲,乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元和0.2万元,问该公司如何分配在甲,乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
【答案】解:设公司在甲电视台和乙电视台做广告的时间分别为![]() 分钟和
分钟和![]() 分钟,总收益为
分钟,总收益为![]() 元,由题意得
元,由题意得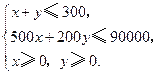
目标函数为![]() .………………4分
.………………4分
二元一次不等式组等价于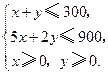
作出二元一次不等式组所表示的平面区域,
即可行域. 如图:
作直线![]() ,
,
即![]() .
.
平移直线![]() ,从图中可知,当直线
,从图中可知,当直线![]() 过
过![]() 点时,目标函数取得最大值.………8分
点时,目标函数取得最大值.………8分
联立![]() 解得
解得![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() (元)
(元)
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元
【解析】试题分析:设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,
总收益为z元,由题意得
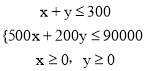 ,
,
目标函数为z=3000x+2000y.
二元一次不等式组等价于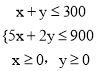
作出二元一次不等式组所表示的平面区域,即可行域.
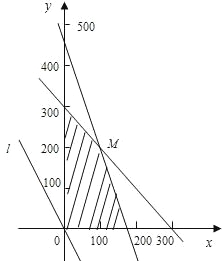
如图,作直线l:3000x+2000y=0,即3x+2y=0.
平移直线l,从图中可知,当直线l过M点时,目标函数取得最大值.
联立![]()
解得x=100,y=200.
∴点M的坐标为(100,200).
∴zmax=3000x+2000y=700000(元)
答:该公司分配在甲乙两个电视台的广告时间分别为100分钟和200分钟时,公司收益最大,最大收益为70万元.


科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1= ![]() ,且前n项的算术平均数等于第n项的2n﹣1倍(n∈N*).
,且前n项的算术平均数等于第n项的2n﹣1倍(n∈N*).
(1)写出此数列的前5项;
(2)归纳猜想{an}的通项公式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a3x+1 , g(x)=( ![]() )5x﹣2 , 其中a>0,且a≠1.
)5x﹣2 , 其中a>0,且a≠1.
(1)若0<a<1,求满足f(x)<1的x的取值范围;
(2)求关于x的不等式f(x)≥g(x)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() ,
, ![]() ,
, ![]() .
.
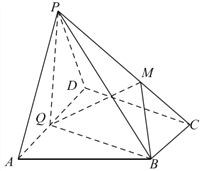
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 大小为
大小为![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴长为半径的圆与直线
的长半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,已知
中,已知![]() 对任意
对任意![]() 都成立,数列
都成立,数列![]() 的前
的前![]() 项和为
项和为![]() .(这里
.(这里![]() 均为实数)
均为实数)
(1)若![]() 是等差数列,求
是等差数列,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() ;
;
(3)是否存在实数![]() ,使数列
,使数列![]() 是公比不为
是公比不为![]() 的等比数列,且任意相邻三项
的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列?若存在,求出所有
按某顺序排列后成等差数列?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex-ax-1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2-e)x.
①求函数h(x)=f (x)-g (x)的单调区间;
②若函数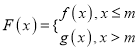 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;
(2)若存在实数x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求证:e-1≤a≤e2-e.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com