Question

【题目】交通拥堵指数是综合反映道路网畅通或拥堵的概念，记交通拥堵指数为 ，其范围为 ，分别有五个级别： 畅通； 基本畅通； 轻度拥堵； 中度拥堵； 严重拥堵．晚高峰时段 ，从某市交通指挥中心选取了市区 个交通路段，依据其交通拥堵指数数据绘制的直方图如图所示．

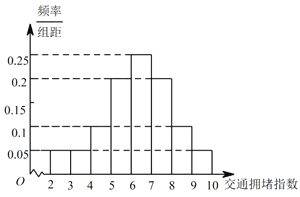
（Ⅰ）求出轻度拥堵，中度拥堵，严重拥堵路段各有多少个；

（Ⅱ）用分层抽样的方法从交通指数在 ， ， 的路段中共抽取个路段，求依次抽取的三个级别路段的个数；

（Ⅲ）从（Ⅱ）中抽取的个路段中任取个，求至少个路段为轻度拥堵的概率．

Answer 1

【答案】(1) 个， 个， 个(2) ， ， 个（3）

【解析】试题分析：（Ⅰ）由频率分布直方图可知底×高=频率，频数×20=个数，由频率分布直方图很容易知道轻度拥堵，中度拥堵，严重拥堵的频率分别是0.3，0.45，0.15，从而得到 个路段中，轻度拥堵、中度拥堵、严重拥堵路段的个数；

（Ⅱ）根据分层抽样，交通指数在[4，10）的路段共18个，抽取6个，求出抽取的比值，继而求得路段个数；

（Ⅲ）考查古典概型，一一列举所有满足条件的基本事件，利用概率公式求得．

试题解析：

（Ⅰ） 由直方图可知：

， ， ．

所以这 个路段中，轻度拥堵、中度拥堵、严重拥堵路段分别为 个， 个， 个．

（Ⅱ） 由（1）知拥堵路段共有 个，按分层抽样从 个路段中选出 个，

每种情况： ， ， ，

即这三个级别路段中分别抽取的个数为 ， ， 个．

（Ⅲ） 记（Ⅱ）中选取的 个轻度拥堵路段为 ， ，

选取的 个中度拥堵路段为 ， ， ，选取的 个严重拥堵路段为 ，

则从 个路段选取 个路段的可能情况如下：

， ， ， ， ， ， ，

， ， ， ， ， ， ， 共 种可能，

其中至少有 个轻度拥堵的有： ， ， ， ， ，

， ， ， 共 种可能．

所以所选 个路段中至少 个路段为轻度拥堵的概率为 ．