
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且 ![]() .
.
(1)求sinB的值;
(2)若D为AC的中点,且BD=1,求△ABD面积的最大值.
【答案】
(1)解:由 ![]() .
.
可得: ![]()
由正弦定理: ![]() .
.
得: ![]() .即cosB=
.即cosB= ![]() .
.
那么:sinB= ![]()
(2)解:由BD=1,运用向量的关系,可得| ![]() |=2|
|=2| ![]() |=2,
|=2,
可得:| ![]() |2+|
|2+| ![]() |2+2
|2+2 ![]() =4,
=4,
则| ![]() |2+|
|2+| ![]() |2+2|
|2+2| ![]() |cosB=4,
|cosB=4,
由余弦定理:得| ![]() |2+|
|2+| ![]() |2=4﹣
|2=4﹣ ![]() ×|
×| ![]() |
|
∵| ![]() |2+|
|2+| ![]() |2≥2|
|2≥2| ![]() ||
|| ![]() |,(当且仅当|
|,(当且仅当| ![]() |=|
|=| ![]() |时取等号)
|时取等号)
∴4﹣ ![]() ×|
×| ![]() |≥2|
|≥2| ![]() ||
|| ![]() |,
|,
∴| ![]() ||
|| ![]() |≤
|≤ ![]() .
.
∴△ABC面积S= ![]() |
| ![]() ||
|| ![]() |sinB≤
|sinB≤ ![]() =
= ![]()
那么:△ABD面积的最大值为 ![]() =
= ![]() .
.
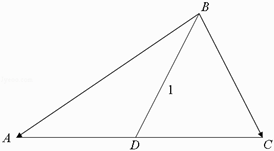
【解析】(1)运用正弦定理和三角形的内角和定理可得cosB,即可得sinB的值.(2)由BD=1,运用向量的关系可得| ![]() |=2|
|=2| ![]() |=2,平方后,可得|
|=2,平方后,可得| ![]() |2+|
|2+| ![]() |2+2
|2+2 ![]() =4利用基本不等式即可求解△ABD面积的最大值.
=4利用基本不等式即可求解△ABD面积的最大值.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】小明家订了一份报纸,送报人可能在早上6 : 30至7 : 30之间把报纸送到小明家,小明离开家去上学的时间在早上7 : 00至8 : 30之间,问小明在离开家前能得到报纸(称为事件![]() )的概率是多少( )
)的概率是多少( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=cosx的图象与直线x= ![]() ,x=
,x= ![]() 以及x轴所围成的图形的面积为a,则(x﹣
以及x轴所围成的图形的面积为a,则(x﹣ ![]() )(2x﹣
)(2x﹣ ![]() )5的展开式中的常数项为(用数字作答).
)5的展开式中的常数项为(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系 ![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为 ![]() ,右顶点为
,右顶点为 ![]() ,设点
,设点 ![]() .
.
(1)求该椭圆的标准方程;
(2)若 ![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段 ![]() 中点
中点 ![]() 的轨迹方程;
的轨迹方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() 的右顶点为A,离心率为e,且椭圆C过点
的右顶点为A,离心率为e,且椭圆C过点 ![]() ,以AE为直径的圆恰好经过椭圆的右焦点.
,以AE为直径的圆恰好经过椭圆的右焦点.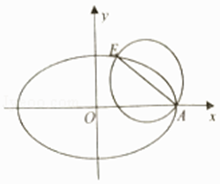
(1)求椭圆C的标准方程;
(2)已知动直线l(直线l不过原点且斜率存在)与椭圆C交于P,Q两个不同的点,且△OPQ的面积S=1,若N为线段PQ的中点,问:在x轴上是否存在两个定点E1 , E2 , 使得直线NE1与NE2的斜率之积为定值?若存在,求出E1 , E2的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
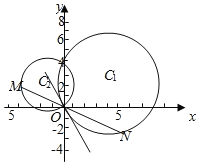
【题目】已知圆![]() 与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
(1)求圆C2的方程;
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在求出定点坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com