
【题目】已知函数f(x)=lnx﹣2ax(其中a∈R).
(Ⅰ)当a=1时,求函数f(x)的图象在x=1处的切线方程;
(Ⅱ)若f(x)≤1恒成立,求a的取值范围;
(Ⅲ)设g(x)=f(x)+ ![]() x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
【答案】解:(Ⅰ)当a=1时,f(x)=lnx﹣2x,则 ![]() ﹣2,x>0, ∴f(1)=﹣2,f′(1)=﹣1,
﹣2,x>0, ∴f(1)=﹣2,f′(1)=﹣1,
∴函数f(x)的图象在x=1处的切线方程为y﹣(﹣2)=﹣(x﹣1),即x+y+1=0.
(Ⅱ)不等式f(x)≤1,即lnx﹣2ax≤1,∴2ax≥lnx﹣1,
∵x>0,∴2a≥ ![]() 恒成立,
恒成立,
令φ(x)= ![]() (x>0),则φ′(x)=
(x>0),则φ′(x)= ![]() ,
,
当0<x<e2时,φ′(x)>0,φ(x)单调递增,当x>e2时,φ′(x)<0,φ(x)单调递减,
∴当x=e2时,φ(x)取得极大值,也为最大值,故φ(x)max=φ(e2)= ![]() ,
,
由2a≥ ![]() ,得a≥
,得a≥ ![]() ,∴实数a的取值范围是[
,∴实数a的取值范围是[ ![]() ,+∞).
,+∞).
(Ⅲ)证明:由g(x)=f(x)+ ![]() x2=
x2= ![]() ,得
,得 ![]() ,
,
①当﹣1≤a≤1时,g(x)单调递增无极值点,不符合题意;
②当a>1或a<﹣1时,令g′(x)=0,设x2﹣2ax+1=0的两根为x0和x′,
∵x0为函数g(x)的极大值点,∴0<x0<x′,
由 ![]() =1,
=1, ![]() ,知a>1,0<x0<1,
,知a>1,0<x0<1,
又由g′(x0)= ![]() =0,得a=
=0,得a= ![]() ,
,
∵ ![]() =﹣
=﹣ ![]() ,0<x0<1,
,0<x0<1,
令h(x)=﹣ ![]() ,x∈(0,1),则
,x∈(0,1),则 ![]() ,
,
令 ![]() ,x∈(0,1),则
,x∈(0,1),则 ![]() ,
,
当 ![]() 时,μ′(x)>0,当
时,μ′(x)>0,当 ![]() 时,μ′(x)<0,
时,μ′(x)<0,
∴μ(x)max=μ( ![]() )=ln
)=ln ![]() <0,∴h′(x)<0,
<0,∴h′(x)<0,
∴h(x)在(0,1)上单调递减,∴h(x)>h(1)=0,
∴x0f(x0)+1+ax02>0.
【解析】(Ⅰ)当a=1时, ![]() ﹣2,由此利用导数的几何意义能求出函数f(x)的图象在x=1处的切线方程.(Ⅱ)由不等式f(x)≤1,得2a≥
﹣2,由此利用导数的几何意义能求出函数f(x)的图象在x=1处的切线方程.(Ⅱ)由不等式f(x)≤1,得2a≥ ![]() 恒成立,令φ(x)=
恒成立,令φ(x)= ![]() (x>0),则φ′(x)=
(x>0),则φ′(x)= ![]() ,由此利用导数性质能求出实数a的取值范围.(Ⅲ)由g(x)=f(x)+
,由此利用导数性质能求出实数a的取值范围.(Ⅲ)由g(x)=f(x)+ ![]() x2=
x2= ![]() ,得
,得 ![]() ,分类讨论求出a=
,分类讨论求出a= ![]() ,由x0f(x0)+1+ax02=﹣
,由x0f(x0)+1+ax02=﹣ ![]() ,令h(x)=﹣
,令h(x)=﹣ ![]() ,x∈(0,1),则
,x∈(0,1),则 ![]() ,利用构造法推导出h′(x)<0,由此能证明x0f(x0)+1+ax02>0.
,利用构造法推导出h′(x)<0,由此能证明x0f(x0)+1+ax02>0.
【考点精析】根据题目的已知条件,利用函数的极值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是 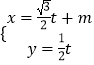 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)设点P(m,0),若直线l与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),则y1 , y2 , …y2017的方差为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x),恒有f(x)=f(2﹣x)成立,且f′(x)(x﹣1)>0,对任意的x1<x2 , 则f(x1)<f(x2)成立的充要条件是( )
A.x2>x1≥1
B.x1+x2>2
C.x1+x2≤2
D.x2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(kx+4)lnx﹣x(x>1),若f(x)>0的解集为(s,t),且(s,t)中只有一个整数,则实数k的取值范围为( )
A.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() )
)
B.( ![]() ﹣2,
﹣2, ![]() ﹣
﹣ ![]() ]
]
C.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1]
﹣1]
D.( ![]() ﹣
﹣ ![]() ,
, ![]() ﹣1)
﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2x+a,g(x)=lnx﹣2x,如果存在 ![]() ,使得对任意的
,使得对任意的 ![]() ,都有f(x1)≤g(x2)成立,则实数a的取值范围是 .
,都有f(x1)≤g(x2)成立,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m≠0,向量 ![]() =(m,3m),向量
=(m,3m),向量 ![]() =(m+1,6),集合A={x|(x﹣m2)(x+m﹣2)=0}.
=(m+1,6),集合A={x|(x﹣m2)(x+m﹣2)=0}.
(1)判断“ ![]() ∥
∥ ![]() ”是“|
”是“| ![]() |=
|= ![]() ”的什么条件
”的什么条件
(2)设命题p:若 ![]() ⊥
⊥ ![]() ,则m=﹣19,命题q:若集合A的子集个数为2,则m=1,判断p∨q,p∧q,¬q的真假,并说明理由.
,则m=﹣19,命题q:若集合A的子集个数为2,则m=1,判断p∨q,p∧q,¬q的真假,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() =1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2
=1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2 ![]() 倍.
倍.
(Ⅰ)求C的离心率;
(Ⅱ)设l的斜率为1,在C上是否存在一点M,使得 ![]() ?若存在,求出点M的坐标;若不存在,说明理由.
?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com