
【题目】为了调查观众对某电视剧的喜爱程度,某电视台在甲乙两地随机抽取了8名观众做问卷调查,得分结果如图所示:
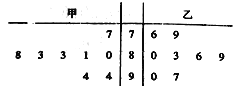
(1)计算甲地被抽取的观众问卷得分的中位数和乙地被抽取的观众问卷得分的平均数;
(2)用频率估计概率,若从乙地的所有观众中再随机抽取4人进行问卷调查,记问卷分数不低于80分的人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知曲线y=x3+x-2在点P0处的切线l1平行于直线4x-y-1=0,且点P0在第三象限.
(1)求P0的坐标;(2)若直线l⊥l1,且l也过切点P0,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
已知函数f(x)=(x2+bx+b)![]() (b∈R).
(b∈R).
(1)当b=4时,求f(x)的极值;
(2)若f(x)在区间![]() 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是
①任取x>0,均有3x>2x .
②当a>0,且a≠1时,有a3>a2 .
③y=( ![]() )﹣x是增函数.
)﹣x是增函数.
④y=2|x|的最小值为1.
⑤在同一坐标系中,y=2x与y=2﹣x的图象关于y轴对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离. 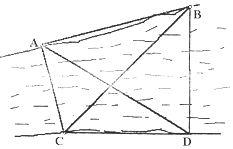
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com