
思路解析:本题考查对直线方程、直线的斜率的理解,及直线的图形的应用,本题要理解在运动过程中各点位置的变化情况.
解:设P0(4,0)、Q0(0,2)、R0(2,1)且将P、Q、R分别看作由P0、Q0、R0同时出发,分别沿x轴正方向,y轴正方向,斜率为1的直线向上方向匀速运动,经过时间t后(t>0),它们的坐标为P(4+at,0)、Q(0,2+bt)、R(2+![]() ,1+
,1+![]() ),则PQ的方程为
),则PQ的方程为![]() =1.
=1.
∵P、Q、R恒在一条直线上,将R代入上式,即[bc+ac-![]() ab]t2+[bc-
ab]t2+[bc-![]() (a+2b)]t=0对一切t>0恒成立.
(a+2b)]t=0对一切t>0恒成立.
∴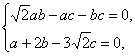
消去c得a2-3ab+2b2=0.
得a=b或a=2b.
当a=b时,c=![]() b,此时a∶b∶c=2∶2∶
b,此时a∶b∶c=2∶2∶![]() ;
;
当a=2b时,c=![]() b,此时a∶b∶c=6∶3∶2
b,此时a∶b∶c=6∶3∶2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com