
【题目】在平行六面体ABCD—A1B1C1D1中,AB=AC,平面BB1C1C⊥底面ABCD,点M、F分别是线段AA1、BC的中点.

(1)求证:AF⊥DD1;
(2)求证:AF∥平面MBC1.
【答案】(1)见证明(2)见证明
【解析】
(1)由题意可得AF⊥BC.再结合平面![]() 底面
底面![]() ,得到AF⊥平面
,得到AF⊥平面![]() ,
,
可得到AF⊥CC1,根据CC1∥DD1,证得AF⊥DD1.
(2)先根据平行六面体中的线线平行,证出四边形AFEM是平行四边形,得到EM // AF,即可证明线面平行.
证明:(1)∵AB![]() AC,点F是线段BC的中点,
AC,点F是线段BC的中点,
∴AF⊥BC.又∵平面![]() 底面
底面![]() ,AF
,AF![]() 平面ABC,
平面ABC,
平面![]() 底面
底面![]() ,
,
∴AF⊥平面![]() .
.
又CC1![]() 平面
平面![]() ,∴AF⊥CC1,
,∴AF⊥CC1,
又CC1∥DD1,∴AF⊥DD1.
(2)连结B1C与BC1交于点E,连结EM,FE.
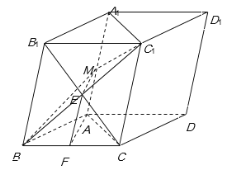
在斜三棱![]() 中,四边形BCC1B1是平行四边形,
中,四边形BCC1B1是平行四边形,
∴点E为B1C的中点.
∵点F是BC的中点,
∴FE//B1B,FE![]() B1B.
B1B.
又∵点M是平行四边形BCC1B1边AA1的中点,
∴AM//B1B,AM![]() B1B.
B1B.
∴AM// FE,AM![]() FE.
FE.
∴四边形AFEM是平行四边形.
∴EM // AF.
又EM![]() 平面MBC1,AF
平面MBC1,AF![]() 平面MBC1,
平面MBC1,
∴AF //平面MBC1.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)证明:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() .
.
(2)是否存在最大的整数![]() ,使得函数
,使得函数![]() 在其定义域上是增函数?若存在,求
在其定义域上是增函数?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年元旦班级联欢晚会上,某班在联欢会上设计了一个摸球表演节目的游戏,在一个纸盒中装有1个红球,1个黄球,1个白球和1个黑球,这些球除颜色外完全相同,A同学不放回地每次摸出1个球,若摸到黑球则停止摸球,否则就要将纸盒中的球全部摸出才停止.规定摸到红球表演两个节目,摸到白球或黄球表演一个节目,摸到黑球不用表演节目.
(1)求A同学摸球三次后停止摸球的概率;
(2)记X为A同学摸球后表演节目的个数,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,公比为q(q≠1).令A=
为等比数列,公比为q(q≠1).令A=![]() .A={1,2},
.A={1,2},
(1)当![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,q>0,试比较
,q>0,试比较![]() 与
与![]() (n≥3)的大小?并证明你的结论.
(n≥3)的大小?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() 为自然对数的底数. 设
为自然对数的底数. 设![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)若![]() 时,函数
时,函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 上的单调区间;
上的单调区间;
(Ⅲ)若![]() ,函数
,函数![]() 在区间
在区间![]() 内有零点,求
内有零点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com