
【题目】已知双曲线![]() :
:![]() 的离心率
的离心率![]() ,其左焦点
,其左焦点![]() 到此双曲线渐近线的距离为
到此双曲线渐近线的距离为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点,且以
两点,且以![]() 为直径的圆
为直径的圆![]() 过原点
过原点![]() ,求圆
,求圆![]() 的圆心到抛物线
的圆心到抛物线![]() 的准线的距离.
的准线的距离.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】今年,新型冠状病毒来势凶猛,老百姓一时间“谈毒色变”,近来,有关喝白酒可以预防病毒的说法一直在民间流传,更有人拿出“医”字的繁体字“醫”进行解读为:医治瘟疫要喝酒,为了调查喝白酒是否有助于预防病毒,我们调查了1000人的喝酒生活习惯与最终是否得病进行了统计,表格如下:
每周喝酒量(两) |
|
|
|
|
|
人数 | 100 | 300 | 450 | 100 |
|
规定:①每周喝酒量达到4两的叫常喝酒人,反之叫不常喝酒人;
②每周喝酒量达到8两的叫有酒瘾的人.
(1)求![]() 值,从每周喝酒量达到6两的人中按照分层抽样选出6人,再从这6人中选出2人,求这2人中无有酒瘾的人的概率;
值,从每周喝酒量达到6两的人中按照分层抽样选出6人,再从这6人中选出2人,求这2人中无有酒瘾的人的概率;
(2)请通过上述表格中的统计数据,填写完下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.1的前提下认为是否得病与是否常喝酒有关?并对民间流传的说法做出你的判断.
列联表,并通过计算判断是否能在犯错误的概率不超过0.1的前提下认为是否得病与是否常喝酒有关?并对民间流传的说法做出你的判断.
常喝酒 | 不常喝酒 | 合计 | |
得病 | |||
不得病 | 250 | 650 | |
合计 |
参考公式: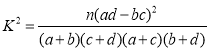 ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知椭圆C:![]() (a>b>0)的短轴长为2,F1,F2分别是椭圆C的左、右焦点,过点F2的动直线与椭圆交于点P,Q,过点F2与PQ垂直的直线与椭圆C交于A、B两点.当直线AB过原点时,PF1=3PF2.
(a>b>0)的短轴长为2,F1,F2分别是椭圆C的左、右焦点,过点F2的动直线与椭圆交于点P,Q,过点F2与PQ垂直的直线与椭圆C交于A、B两点.当直线AB过原点时,PF1=3PF2.
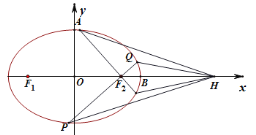
(1)求椭圆的标准方程;
(2)若点H(3,0),记直线PH,QH,AH,BH的斜率依次为![]() ,
,![]() ,
,![]() ,
,![]() .
.
①若![]() ,求直线PQ的斜率;
,求直线PQ的斜率;
②求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图![]() ,
,![]() ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知
,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知![]() .
.
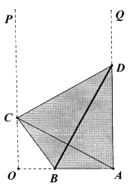
(1)若![]() ,求BD的长;
,求BD的长;
(2)问点C在何处时,规划区域的面积最小?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重(单位:![]() )情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
)情况如柱形图1所示,经过四个月的健身后,他们的体重情况如柱形图2所示.对比健身前后,关于这20名肥胖者,下面结论正确的是( )
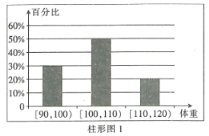
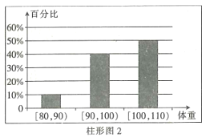
A.他们健身后,体重在区间![]() 内的人数增加了2个
内的人数增加了2个
B.他们健身后,体重在区间![]() 内的人数没有改变
内的人数没有改变
C.因为体重在![]() 内所占比例没有发生变化,所以说明健身对体重没有任何影响
内所占比例没有发生变化,所以说明健身对体重没有任何影响
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,第一次检测厂家的每件产品合格的概率为![]() ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为![]() ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收.
![]() 求某件产品能出厂的概率;
求某件产品能出厂的概率;
![]() 若该产品的生产成本为
若该产品的生产成本为![]() 元/件,出厂价格为
元/件,出厂价格为![]() 元/件,每次检测费为
元/件,每次检测费为![]() 元/件,技术处理每次
元/件,技术处理每次![]() 元/件,回收获利
元/件,回收获利![]() 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记![]() 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com