
【题目】已知函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() ,且
,且![]() ,记点
,记点![]() ,
, ![]() .
.
(Ⅰ)求直线![]() 的方程;
的方程;
(Ⅱ)证明:线段![]() 与曲线
与曲线![]() 有且只有一个异于
有且只有一个异于![]() 、
、![]() 的公共点.
的公共点.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】【试题分析】(1)先求函数的极值点,再求两极值点的坐标,运用直线的点斜式方程求出其方程;(2)依据题设条件先构造函数将问题进行等价转化,再借助导数的知识分析推证:
(Ⅰ)令![]() ,解得
,解得![]() 或
或![]() ,
,
且![]() 在区间
在区间![]() ,
, ![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,即
,即![]() ,
, ![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为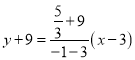 ,化简得
,化简得![]() .
.
(Ⅱ)设![]()
![]()
![]()
![]() ,
,
则线段![]() 与曲线
与曲线![]() 的公共点即
的公共点即![]() 在区间
在区间![]() 上的零点.
上的零点.
令![]()
![]() ,解得
,解得![]() ,
, ![]() ,
,
且![]() 在区间
在区间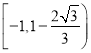 ,
, 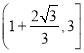 上单调递增,在区间
上单调递增,在区间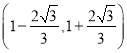 上单调递减.
上单调递减.
![]() 由
由![]()
![]() 可得
可得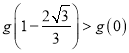
![]()
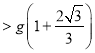 ,
,
即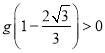 ,
, 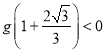 ,
,
![]() 在区间
在区间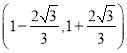 上有且仅有有一个零点.
上有且仅有有一个零点.
当![]() 时,有
时,有![]() ,
, ![]() 在
在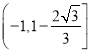 上无零点;
上无零点;
当![]() 时,有
时,有![]() ,
, ![]() 在
在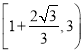 上无零点;
上无零点;
综上, ![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
所以线段![]() 与曲线
与曲线![]() 有且只有一个异于
有且只有一个异于![]() 、
、![]() 的公共点.
的公共点.


科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,AD=![]() 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
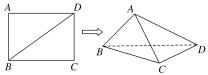
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列是关于函数y=f(x),x∈[a,b]的几个命题:
①若x0∈[a,b]且满足f(x0)=0,则(x0,0)是f(x)的一个零点;
②若x0是f(x)在[a,b]上的零点,则可用二分法求x0的近似值;
③函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点;
④用二分法求方程的根时,得到的都是近似值.
那么以上叙述中,正确的个数为 ( )
A. 0 B. 1 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沭阳县某水果店销售某种水果,经市场调查,该水果每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() 近似满足关系式
近似满足关系式![]() ,其中
,其中![]() 为常数,已知销售价格定为
为常数,已知销售价格定为![]() 元
元![]() 千克时,每日可销售出该水果
千克时,每日可销售出该水果![]() 千克.
千克.
(1)求实数![]() 的值;
的值;
(2)若该水果的成本价格为![]() 元
元![]() 千克,要使得该水果店每日销售该水果获得最大利润,请你确定销售价格
千克,要使得该水果店每日销售该水果获得最大利润,请你确定销售价格![]() 的值,并求出最大利润.
的值,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有将;某顾客从此10张券中任取2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值![]() (元)的概率分布列.
(元)的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=
=1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=![]() (a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元/件的新产品,规定试销时销售单价不低于成本单价,又不高于800元/件.经试销调查,发现销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)可近似看作一次函数
(元/件)可近似看作一次函数![]() 的关系(如图所示).
的关系(如图所示).
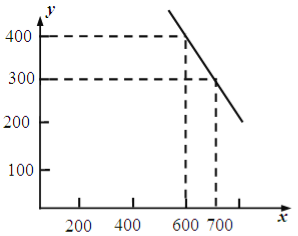
(1)根据图象,求一次函数![]() 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价—成本总价)为![]() 元. 试用销售单价
元. 试用销售单价![]() 表示毛利润
表示毛利润![]() 并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
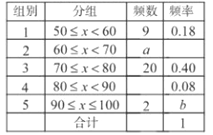

请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出![]() 的值;
的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用:列表法或树状图求出小明、小敏同时被选中的概率.(注:五位同学请用![]() 表示,其中小明为
表示,其中小明为![]() ,小敏为
,小敏为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据完成下面2×2列联表;
(2)请问能有多大把握认为药物有效?
不得禽流感 | 得禽流感 | 总计 | |
服药 | |||
不服药 | |||
总计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com