
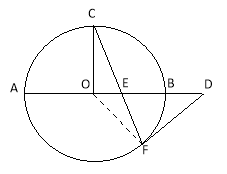
【题目】如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
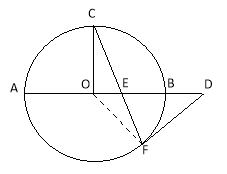
(1)求证:DE2=DBDA;
(2)若DB=2,DF=4,试求CE的长.
【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)由切割线定理有![]() ,因此只要证明
,因此只要证明![]() ,也即只要证明
,也即只要证明![]() ,再考虑它们的余角是否相等即得;(2)由(1)可得
,再考虑它们的余角是否相等即得;(2)由(1)可得![]() 的长,从而有圆的半径
的长,从而有圆的半径![]() ,再得
,再得![]() ,最后由勾股定理可得
,最后由勾股定理可得![]() .
.
试题解析:(1)证明:连接OF.
因为DF切⊙O于F,所以∠OFD=90°.
所以∠OFC+∠CFD=90°.
因为CO⊥AB于O,所以∠OCF+∠CEO=90°.
所以∠CFD=∠CEO=∠DEF,所以DF=DE.
因为DF是⊙O的切线,所以DF2=DBDA.
所以DE2=DBDA.
(2)解:![]() DF2=DBDA,DB=2,DF=4.
DF2=DBDA,DB=2,DF=4.
![]() DA=8,从而AB=6,则
DA=8,从而AB=6,则![]() .
.
又由(1)可知,DE=DF=4,![]() BE=2,OE=1.
BE=2,OE=1.
从而在![]() 中,
中,![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某家具厂生产一种课桌,每张课桌的成本为50元,出厂单价为80元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部课桌出厂单价降低0.02元.根据市场调查,销售商一次订购量不会超过1000张.
(Ⅰ)设一次订购量为![]() 张,课桌的实际出厂单价为
张,课桌的实际出厂单价为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(Ⅱ)当一次性订购量![]() 为多少时,该家具厂这次销售课桌所获得的利润
为多少时,该家具厂这次销售课桌所获得的利润![]() 最大?其最大利润是多少元?(该家具厂出售一张课桌的利润=实际出厂单价-成本)
最大?其最大利润是多少元?(该家具厂出售一张课桌的利润=实际出厂单价-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中真命题的个数为( )
①平行于同一平面的两直线平形;②平行于同一平面的两个平面平行;
③垂直于同一平面的两直线平行;④垂直于同一平面的两平面垂直;
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)若![]() 在区间
在区间![]() 上是减函数,且对任意的
上是减函数,且对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,且对任意的
,且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com