
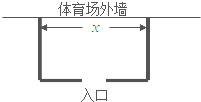
 ������Ŀ�İ������籭���������ݱ�Ľ��У�Ϊȷ���ܾ�����˳�����У���ί�������λ����Լ����¬��������������������ʱΧ��һ�����ι��ں����������Ϊ72m2����ͼ��ʾ����Ҫ����γ��ص�һ����������������ǽ������������������Χ������Ҫ����������ǽ������һ������Ϊ2m����ڣ�����֪�����˵����÷���Ϊ100Ԫ/m����þ�������ij�Ϊx����λ��m�������������˵��ܷ���Ϊy����λ��Ԫ��
������Ŀ�İ������籭���������ݱ�Ľ��У�Ϊȷ���ܾ�����˳�����У���ί�������λ����Լ����¬��������������������ʱΧ��һ�����ι��ں����������Ϊ72m2����ͼ��ʾ����Ҫ����γ��ص�һ����������������ǽ������������������Χ������Ҫ����������ǽ������һ������Ϊ2m����ڣ�����֪�����˵����÷���Ϊ100Ԫ/m����þ�������ij�Ϊx����λ��m�������������˵��ܷ���Ϊy����λ��Ԫ��| 72 |
| x |
| 72 |
| x |
| 144 |
| x |
| 144 |
| 144 |
| x |


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
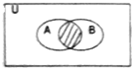 ��֪ȫ��U=R������A={y|y=sinx��x��R}��B={x|x2-x��0}�Ĺ�ϵ��Τ��ͼ��vean����ͼ��ʾ������Ӱ���ֱ�ʾ�ļ����ǣ�������
��֪ȫ��U=R������A={y|y=sinx��x��R}��B={x|x2-x��0}�Ĺ�ϵ��Τ��ͼ��vean����ͼ��ʾ������Ӱ���ֱ�ʾ�ļ����ǣ�������| A��{x|-1��x��1} |
| B��{x|-1��x��1} |
| C��{x|0��x��1} |
| D��{x|0��x��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x1+x2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��1��2��3 | ||
| B��2��3��4 | ||
| C��3��4��5 | ||
D��1��
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��y=log2��x2-2x-3�� | ||
| B��y=x2+x+2 | ||
C��y=
| ||
| D��y=22x+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| 1 |
| x-1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com