
分析 (Ⅰ)设z=a+bi(a,b∈R),而|z|=1+3i-z,化为$\sqrt{{a}^{2}+{b}^{2}}$-1-3i+a+bi=0,利用复数相等即可得出.
(II)利用复数的运算法则、共轭复数的定义即可得出.
解答 解:(Ⅰ)设z=a+bi(a,b∈R),而|z|=1+3i-z,
∴$\sqrt{{a}^{2}+{b}^{2}}$-1-3i+a+bi=0,
则$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{b}^{2}}+a-1=0}\\{b-3=0}\end{array}\right.$,解得a=-4,b=3.
∴z=-4+3i.
(Ⅱ)z1=$\frac{(1+i)^{2}(-7+24i)}{2z}$=$\frac{2i(-7+24i)}{2(-4+3i)}$=$\frac{24+7i}{4-3i}$=$\frac{(24+7i)(4+3i)}{(4-3i)(4+3i)}$=$\frac{75+100i}{25}$=3+4i,
∴$\overline{{z}_{1}}$=3-4i.
点评 本题考查了复数的运算法则、共轭复数的定义、复数相等、模的计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
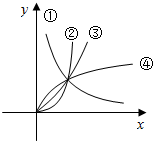 如图表示的是四个幂函数在同一坐标系中第一象限内的图象,则幂函数y=x${\;}^{\frac{1}{2}}$的图象是( )
如图表示的是四个幂函数在同一坐标系中第一象限内的图象,则幂函数y=x${\;}^{\frac{1}{2}}$的图象是( )| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2\sqrt{x}}}$ | B. | $\frac{1}{{\sqrt{x}}}$ | C. | $\frac{2}{x}$ | D. | $\frac{1}{2x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ①② | D. | 都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com