
【题目】下列命题:①集合![]() 的子集个数有
的子集个数有![]() 个;②定义在
个;②定义在![]() 上的奇函数
上的奇函数![]() 必满足
必满足![]() ;③
;③![]() 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与![]() 轴相交;⑤
轴相交;⑤![]() 在
在![]() 上是减函数,其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
上是减函数,其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
【答案】①②
【解析】①集合![]() 的子集个数有
的子集个数有![]() 个,①正确;②定义在
个,①正确;②定义在![]() 上的奇函数
上的奇函数![]() 其图象关于原点对称,故必满足
其图象关于原点对称,故必满足![]() ,②正确;③
,②正确;③![]()
![]() ,其图象关于
,其图象关于![]() 轴对称,是偶函数,③错误;④
轴对称,是偶函数,③错误;④![]() 的图象与
的图象与![]() 轴没有交点,但它是偶函数,④错误;⑤取
轴没有交点,但它是偶函数,④错误;⑤取![]() ,虽然
,虽然![]() ,但
,但![]() ,不符合减函数定义,⑤错误,故答案为①②.
,不符合减函数定义,⑤错误,故答案为①②.
【 方法点睛】本题主要通过对多个命题真假的判断,主要考查集合的子集、函数的单调性、函数的奇偶性、函数的图象与性质,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意先从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.


科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg)其频率分布直方图如下:

(1) 记![]() 表示事件“旧养殖法的箱产量低于50kg”,估计
表示事件“旧养殖法的箱产量低于50kg”,估计![]() 的概率;
的概率;
(2)填写下面联表,并根据列联表判断是否有![]() %的把握认为箱产量与养殖方法有关:
%的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,且存在实常数
,且存在实常数![]() ,使得对于定义域内任意
,使得对于定义域内任意![]() ,都有
,都有![]() 成立,则称此函数
成立,则称此函数![]() 具有“性质
具有“性质![]() ”.
”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,求出所有
性质”,求出所有![]() 的值的集合,若不具有“
的值的集合,若不具有“![]() 性质”,请说明理由;
性质”,请说明理由;
(2)已知函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)已知函数![]() 既具有“
既具有“![]() 性质”,又具有“
性质”,又具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 有2017个公共点,求实数
有2017个公共点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(cos2ωx-sin2ωx,sinωx),b=(![]() ,2cosωx),设函数f(x)=a·b(x∈R)的图象关于直线x=
,2cosωx),设函数f(x)=a·b(x∈R)的图象关于直线x=![]() 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1).
(1)求函数f(x)的最小正周期和单调递增区间;
(2)若将y=f(x)图象上各点的横坐标变为原来的![]() ,再将所得图象向右平移
,再将所得图象向右平移![]() 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在![]() 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
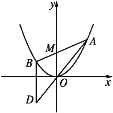
(1)证明动点D在定直线上;
(2)作C的任意一条切线l(不含x轴),与直线y=2相交于点N1,与(1)中的定直线相交于点N2,证明|MN2|2-|MN1|2为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2cos2x的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若函数g(x)在区间[0,
个单位后得到函数g(x)的图象,若函数g(x)在区间[0, ![]() ]和[2a,
]和[2a, ![]() ]上均单调递增,则实数a的取值范围是( )
]上均单调递增,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com