
【题目】如图,四棱锥![]() 的底面是正方形,
的底面是正方形,![]() 平面
平面![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由![]() 平面
平面![]() 及底面
及底面![]() 是正方形可证得
是正方形可证得![]() 平面
平面![]() ,则
,则![]() ,又由
,又由![]() ,即可求证;
,即可求证;
(2)以![]() 为原点,分别以
为原点,分别以![]() 所在的直线为x轴、y轴、z轴建立空间直角坐标系
所在的直线为x轴、y轴、z轴建立空间直角坐标系![]() ,由(1)可知
,由(1)可知![]() 为平面
为平面![]() 的一个法向量,求得平面
的一个法向量,求得平面![]() 的一个法向量
的一个法向量![]() ,进而利用数量积求解即可
,进而利用数量积求解即可
(1)证明:因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,
因为底面![]() 是正方形,所以
是正方形,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]()
(2)因为![]() 平面
平面![]() ,底面
,底面![]() 为正方形,
为正方形,
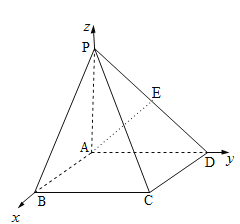
所以![]() ,以
,以![]() 为原点,分别以
为原点,分别以![]() 所在的直线为x轴、y轴、z轴建立空间直角坐标系
所在的直线为x轴、y轴、z轴建立空间直角坐标系![]() (如图所示),
(如图所示),
设![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
所以![]() ,
,
由(1)得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,所以
,所以![]() ,
,
因此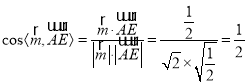 ,
,
由图可知二面角![]() 的大小为钝角,
的大小为钝角,
故二面角![]() 的余弦值为
的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
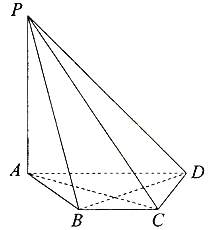
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明初出现了一大批杰出的骑兵将领,比如徐达、常遇春、李文忠、蓝玉和朱棣.明初骑兵军团击败了不可一世的蒙古骑兵,是当时世界上最强骑兵军团.假设在明军与元军的某次战役中,明军有8位将领,善用骑兵的将领有5人;元军有8位将领,善用骑兵的有4人.
(1)现从明军将领中随机选取4名将领,求至多有3名是善用骑兵的将领的概率;
(2)在明军和元军的将领中各随机选取2人,![]() 为善用骑兵的将领的人数,写出
为善用骑兵的将领的人数,写出![]() 的分布列,并求
的分布列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“创文创卫”活动中,某机构为了解一小区成年居民“吸烟与性别”是否有关.从该小区中随机抽取200位成年居民,得到下边列联表:已知在全部200人中随机抽取1人,抽到不吸烟的概率为0.75.
吸烟 | 不吸烟 | 合计 | |
男 | 40 | ||
女 | 90 | ||
合计 | 200 |
(1)补充上面的列联表,并判断:能否有99.9%的把握认为“吸烟与性别”有关;
(2)用分层抽样的方法从吸烟居民中选5人出来,然后再从中抽2人出来,给小区居民谈谈吸烟的危害性,求恰好抽到“一男一女”的概率.
参考公式:  .
.
参考数据:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com