
分析 变形利用减函数的定义即可证明.
解答 解:f(x)=$\frac{2-x}{x+2}$=$\frac{4}{x+2}$-1,
?x1,x2∈(-2,+∞),且x1<x2.
∴f(x1)-f(x2)=$\frac{4}{{x}_{1}+2}-1$-$(\frac{4}{{x}_{2}+2}-1)$=$\frac{4({x}_{2}-{x}_{1})}{({x}_{1}+2)({x}_{2}+2)}$,
∵x1,x2∈(-2,+∞),且x1<x2.
∴x1+2>0,x2+2>0,x2-x1>0,
∴$\frac{4({x}_{2}-{x}_{1})}{({x}_{1}+2)({x}_{2}+2)}$>0,
∴f(x1)>f(x2),
∴函数f(x)=$\frac{2-x}{x+2}$在(-2,+∞)上是减函数.
点评 本题考查了减函数的定义,考查了推理能力与计算能力,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
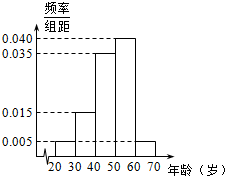 跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.
跳广场舞是现在广大市民喜爱的户外健身运动,某健身运动公司为了解本地区市民对跳广场舞的热衷程度,随机抽取了100名跳广场舞的市民,统计其年龄(单位:岁)并整理得到如下的频率分布直方图(其中年龄的分组区间分别为[20,30),[30,40),[40,50),[50,60),[60,70]),其中女性市民有55名,将所抽样本中年龄不小于50岁跳广场舞的市民称为“广舞迷”.已知其中有30名女性广舞迷.| 广舞迷 | 非广舞迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com