
分析 (1)求出函数f(x)的导数,得到sinx+cosx-e<0,从而求出函数的单调性即可;
(2)问题转化为证明任意x∈[0,+∞),six-ax2+2a-e<0,设g(a)=sinx-ax2+2a-e=(-x2+2)a+sinx-e,看作以a为变量的一次函数,结合三角函数的性质证明即可.
解答 解:(1)a=0时,f(x)=ex(sinx-e),
则f′(x)=ex(sinx-e+cosx),
∵sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)≤$\sqrt{2}$<e,
∴sinx+cosx-e<0,
故f′(x)<0,
则f(x)在R递减;
(2)证明:当x≥0时,y=ex≥1,
要证明对任意的x∈[0,+∞),f(x)<0,
则只需证明任意x∈[0,+∞),six-ax2+2a-e<0,
设g(a)=sinx-ax2+2a-e=(-x2+2)a+sinx-e,
看作以a为变量的一次函数,
要使sinx-ax2+2a-e<0,
则$\left\{\begin{array}{l}{g(\frac{1}{2})<0}\\{g(1)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{sinx-{\frac{1}{2}x}^{2}+1-e<0①}\\{sinx{-x}^{2}+2-e<0②}\end{array}\right.$,
∵sinx+1-e<0恒成立,
∴①恒成立,
对于②,令h(x)=sinx-x2+2-e,
则h′(x)=cosx-2x,
设x=t时,h′(x)=0,即cost-2t=0,
∴t=$\frac{cost}{2}$<$\frac{1}{2}$,sint<sin$\frac{π}{6}$=$\frac{1}{2}$,
∴h(x)在(0,t)上,h′(x)>0,h(x)递增,
在(t,+∞)上,h′(x)<0,h(x)递减,
则x=t时,h(x)取得最大值h(t)=sint-t2+2-e
=sint-${(\frac{cost}{2})}^{2}$+2-e=${(\frac{sint}{2}+1)}^{2}$+$\frac{3}{4}$-e≤${(\frac{5}{4})}^{2}$+$\frac{3}{4}$-e=$\frac{27}{16}$-e<0,
故②成立,
综上,在区间[0,+∞)上恒有f(x)<0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及三角函数的性质,是一道综合题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{33}{65}$ | B. | -$\frac{63}{65}$ | C. | -$\frac{33}{65}$ | D. | $\frac{63}{65}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $-\frac{1}{3}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
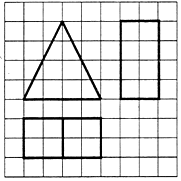
| A. | 16 | B. | $24+8\sqrt{5}$ | C. | 48 | D. | $24+16\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com