解:(1)因为椭圆C的焦点为F
1(0,3),∴b
2=a
2+9,则椭圆C的方程为
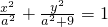
∵M(x,4)(x>0)椭圆C上一点,△MOF
1的面积为

∴
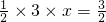
,∴x=1,∴M(1,4)
代入椭圆C的方程
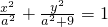
,可得
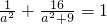
∴a
4-8a
2-9=0
∴a
2=9
∴椭圆C的方程为
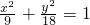
;
(2)假设存在符合题意的直线l存在,设直线方程为y=4x+m,代入椭圆方程,消去y,可得18x
2+8mx+m
2-18=0
设A(x
1,y
1),B(x
2,y
2),则x
1+x
2=-
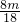
,x
1x
2=
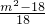
,
因为以线段AB为直径的圆恰好经过原点,所以

∴x
1x
2+y
1y
2=0.
∴x
1x
2+16x
1x
2+4m(x
1+x
2)+m
2=0
∴17×
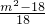
-4m×
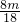
+m
2=0
∴

此时△=64m
2-72(m
2-18)>0
∴直线方程为y=4x
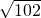
.
分析:(1)根据椭圆C的焦点为F
1(0,3),可得椭圆C的方程为
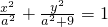
,利用M(x,4)(x>0)椭圆C上一点,△MOF
1的面积为

,求出M的坐标代入椭圆C的方程,即可确定椭圆C的方程;
(2)假设存在符合题意的直线l存在,设直线方程代入椭圆方程,消去y,可得一元二次方程,利用韦达定理,结合以线段AB为直径的圆恰好经过原点,

,即可求得结论.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,确定椭圆方程,正确运用韦达定理是关键.

 +
+ =1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为
=1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为 .
.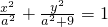

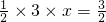 ,∴x=1,∴M(1,4)
,∴x=1,∴M(1,4)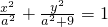 ,可得
,可得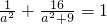
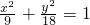 ;
;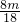 ,x1x2=
,x1x2=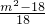 ,
,
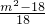 -4m×
-4m×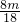 +m2=0
+m2=0
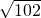 .
.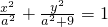 ,利用M(x,4)(x>0)椭圆C上一点,△MOF1的面积为
,利用M(x,4)(x>0)椭圆C上一点,△MOF1的面积为 ,求出M的坐标代入椭圆C的方程,即可确定椭圆C的方程;
,求出M的坐标代入椭圆C的方程,即可确定椭圆C的方程; ,即可求得结论.
,即可求得结论.
