
【题目】下列说法正确的是( )
A.命题p:“ ![]() ”,则?p是真命题
”,则?p是真命题
B.命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0”
C.“x=﹣1”是“x2+2x+3=0”的必要不充分条件
D.“a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件
【答案】D
【解析】解:A.∵sinx+cosx= ![]() ,∴sinx+cosx
,∴sinx+cosx ![]() 成立,即p为真命题,则¬p为假命题,∴A错误. B.根据特称命题的否定是特称命题可知:命题“x∈R使得x2+2x+3<0”的否定是:“x∈R,x2+2x+3≥0”,∴B错误.
成立,即p为真命题,则¬p为假命题,∴A错误. B.根据特称命题的否定是特称命题可知:命题“x∈R使得x2+2x+3<0”的否定是:“x∈R,x2+2x+3≥0”,∴B错误.
C.∵△=4﹣4×3=﹣8<0,∴x2+2x+3=0方程无解,∴C错误.
D.根据对数函数的性质可知,若a>1时,f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数,成立.
若f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数,则a>1.
∴“a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件,∴D正确.
故选D.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2=4
(t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2=4 ![]() ρsin(θ+
ρsin(θ+ ![]() )﹣4.
)﹣4.
(Ⅰ)求曲线C2的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)若曲线C1与曲线C2交于A、B两点,求|AB|的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=cos(2x+ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位后,得到f(x)的图象,则( )
个单位后,得到f(x)的图象,则( )
A.f(x)=﹣sin2x
B.f(x)的图象关于x=﹣ ![]() 对称
对称
C.f( ![]() )=
)= ![]()
D.f(x)的图象关于( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知左、右焦点分别为F1(﹣c,0),F2(c,0)的椭圆 ![]() 过点
过点 ![]() ,且椭圆C关于直线x=c对称的图形过坐标原点.
,且椭圆C关于直线x=c对称的图形过坐标原点.
(I)求椭圆C的离心率和标准方程.
(II)圆 ![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆P1的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆P1的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前 n 项和为 Sn , a1=1,且 an+1=2Sn+1,n∈N .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令 c=log3a2n , bn= ![]() ,记数列{bn}的前 n 项和为Tn , 若对任意 n∈N , λ<Tn 恒成立,求实数 λ 的取值范围.
,记数列{bn}的前 n 项和为Tn , 若对任意 n∈N , λ<Tn 恒成立,求实数 λ 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2
=(2 ![]() cosx,cosx),
cosx,cosx), ![]() =(sinx,2cosx)(x∈R),设函数f(x)=
=(sinx,2cosx)(x∈R),设函数f(x)= ![]()
![]() ﹣1. (Ⅰ)求函数f(x)的单调减区间;
﹣1. (Ⅰ)求函数f(x)的单调减区间;
(Ⅱ)已知锐角△ABC的三个内角分别为A,B,C,若f(A)=2,B= ![]() ,边AB=3,求边BC.
,边AB=3,求边BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级” (Ⅰ)求乙班总分超过甲班的概率
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分
①请你从平均分光和方差的角度来分析两个班的选手的情况;
②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为ξ,求ξ的分布列及数学期望.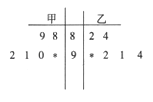
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(Ⅱ)若A,B分别为曲线C1 , C2上的动点,当|AB|取最大值时,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com