
【题目】(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(![]() ,
,![]() ),记∠COA=α.
),记∠COA=α.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求cos∠COB的值.
科目:高中数学 来源: 题型:
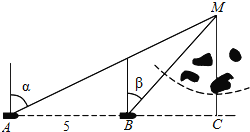
【题目】如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
(1)若α=2β=60°,问该船有无触礁危险?
(2)当α与β满足什么条件时,该船没有触礁的危险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接春节,某工厂大批生产小孩具—— 拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了10次试验,测得的数据如下:
拼图数
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)画出散点图,并判断![]() 与
与![]() 是否具有线性相关关系;
是否具有线性相关关系;

(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, ![]() .
.
参考数据 | 合计 | ||||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 550 |
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 | 917 |
| 100 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | 38500 |
| 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8840 | 10350 | 12200 | 55950 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场预计全年分批购入每台2000元的电视机共3600台.每批都购入![]() 台(
台(![]() 是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线l:y=kx+![]() 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com