
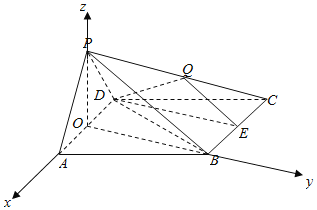
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,![]() ,E是BC中点,点Q在侧棱PC上.
,E是BC中点,点Q在侧棱PC上.
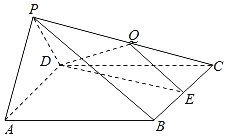
(Ⅰ)求证:AD⊥PB;
(Ⅱ)若Q是PC中点,求二面角E﹣DQ﹣C的余弦值;
(Ⅲ)是否存在Q,使PA∥平面DEQ?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(Ⅰ)证明见解析(Ⅱ)![]() (Ⅲ)存在,
(Ⅲ)存在,![]()
【解析】
(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .推导出
.推导出![]() .,
.,![]() .从而
.从而![]() 平面
平面![]() .由此能证明
.由此能证明![]() .
.
(Ⅱ)以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() 利用向量法能求出二面角
利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(Ⅲ)设![]() ,
,![]() ,推导出
,推导出![]() ,利用向量法能求出当
,利用向量法能求出当![]() 时,
时,![]() 平面
平面![]() .
.
证明:(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
因为菱形![]() 中,
中,![]() ,所以
,所以![]() .
.
所以![]() .
.
因为![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]()
所以![]() .
.
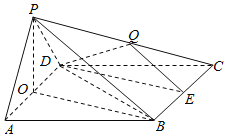
解:(Ⅱ)由(Ⅰ)可知,![]() ,
,![]() ,
,
因为侧面![]() 底面
底面![]() ,且平面
,且平面![]() 底面
底面![]() ,
,![]() 面
面![]()
所以![]() 底面
底面![]() .
.
以![]() 为坐标原点,如图建立空间直角坐标系
为坐标原点,如图建立空间直角坐标系![]() .
.
则![]() ,
,
因为![]() 为
为![]() 中点,所以
中点,所以![]() .
.
所以![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() .
.
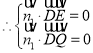 即
即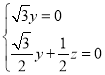
所以平面![]() 的法向量为
的法向量为![]() .
.
因为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则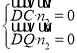 ,即
,即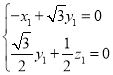 .
.
令![]() ,则
,则![]() ,即
,即![]() .
.
所以![]() .
.
由图可知,二面角![]() 为锐角,所以余弦值为
为锐角,所以余弦值为![]() .
.
(Ⅲ)设![]()
由(Ⅱ)可知![]() .
.
设![]() ,则
,则![]() ,
,
又因为![]() ,
,
所以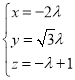 ,即
,即![]() .
.
所以在平面![]() 中,
中,![]() ,
,
所以平面![]() 的法向量为
的法向量为![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
即![]() ,解得
,解得![]() .
.
所以当![]() 时,
时,![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲乙两地相距100海里,船从甲地匀速驶到乙地,已知某船的最大船速是36海里/时:当船速不大于每小时30海里/时,船每小时使用的燃料费用和船速成正比;当船速不小于每小时30海里/时,船每小时使用的燃料费用和船速的平方成正比;当船速为30海里/时,它每小时使用的燃料费用为300元;其余费用(不论船速为多少)都是每小时480元;
(1)试把每小时使用的燃料费用P(元)表示成船速v(海里/时)的函数;
(2)试把船从甲地行驶到乙地所需要的总费用Y表示成船速v的函数;
(3)当船速为每小时多少海里时,船从甲地到乙地所需要的总费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等.
的距离相等.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设动直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
证明:以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“
为“![]() ﹣摆动数列”.
﹣摆动数列”.
(1)设![]() ,
,![]() ,
,![]() ,判断数列
,判断数列![]() 、
、![]() 是否为“
是否为“![]() ﹣摆动数列”,并说明理由;
﹣摆动数列”,并说明理由;
(2)已知“![]() ﹣摆动数列”
﹣摆动数列”![]() 满足:
满足:![]() ,
,![]() .求常数
.求常数![]() 的值;
的值;
(3)设![]() ,
,![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() .求证:数列
.求证:数列![]() 是“
是“![]() ﹣摆动数列”,并求出常数
﹣摆动数列”,并求出常数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(
,(![]() )
)
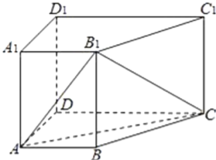
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值;
的值;
(3)现将与四棱柱![]() 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为![]() ,写出
,写出![]() 的解析式.(直接写出答案,不必说明理由)
的解析式.(直接写出答案,不必说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b是不相等的两个正数,在a,b之间插入两组实数:x1,x2,…,xn和y1,y2,…,yn,(n∈N*,且n≥2),使得a,x1,x2,…,xn,b成等差数列,a,y1,y2,…,yn,b成等比数列,给出下列四个式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定成立的是( )
.其中一定成立的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com