
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)![]() 有极大值
有极大值![]() ,函数
,函数![]() 有极小值
有极小值![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)求极值,可先求得导数![]() ,然后通过解不等式
,然后通过解不等式![]() 确定增区间,解不等式
确定增区间,解不等式![]() 确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记
确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记![]() ,求出其导数
,求出其导数![]() ,可知
,可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,这是
,这是![]() 时最小值,
时最小值,![]() ,这是
,这是![]() 时的最大值,因此要证明题中不等式,可分类,
时的最大值,因此要证明题中不等式,可分类,![]() 和
和![]() 分别证明.
分别证明.
试题解析:(1)依题意,![]() ,
,
故![]() ,
,
令![]() ,则
,则![]() 或
或![]() ; 令
; 令![]() ,则
,则![]() ,
,
故当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() .
.
(2) 由(1)知![]() ,令
,令![]() ,
,
则![]() ,
,
可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,令
上单调递减,令![]() .
.
① 当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的图象在
的图象在![]() 图象的上方.
图象的上方.
② 当![]() 时,函数
时,函数![]() 单调递减,所以其最小值为
单调递减,所以其最小值为![]() 最大值为2,而
最大值为2,而![]() ,所以函数
,所以函数![]() 的图象也在
的图象也在![]() 图象的上方.
图象的上方.
综上可知,当![]() 时,
时,![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
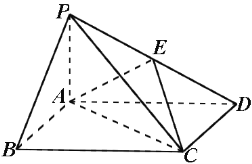
【题目】【2014高考课标2理数18】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 和
和![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: 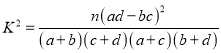 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(3﹣ax)(a>0,a≠1)
(1)当a=3时,求函数f(x)的定义域;
(2)若g(x)=f(x)﹣loga(3+ax),请判定g(x)的奇偶性;
(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+k,且log2f(a)=2,f(log2a)=k,a>0,且a≠1.
(1)求a,k的值;
(2)当x为何值时,f(logax)有最小值?求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料,回答后面问题:
在2014年12月30日![]() 播出的“新闻直播间”节目中,主持人说:“……加入此次亚航失联航班
播出的“新闻直播间”节目中,主持人说:“……加入此次亚航失联航班![]() 被证实失事的话,2014年航空事故死亡人数将达到1320人.尽管如此,航空安全专家还是提醒:飞机仍是相对安全的交通工具.①世界卫生组织去年公布的数据显示,每年大约有124万人死于车祸,而即使在航空事故死亡人数最多的一年,也就是1972年,其死亡数字也仅为3346人;②截至2014年9月,每百万架次中有2.1次(指飞机失事),乘坐汽车的百万人中其死亡人数在100人左右.”
被证实失事的话,2014年航空事故死亡人数将达到1320人.尽管如此,航空安全专家还是提醒:飞机仍是相对安全的交通工具.①世界卫生组织去年公布的数据显示,每年大约有124万人死于车祸,而即使在航空事故死亡人数最多的一年,也就是1972年,其死亡数字也仅为3346人;②截至2014年9月,每百万架次中有2.1次(指飞机失事),乘坐汽车的百万人中其死亡人数在100人左右.”
对上述航空专家给出的①、②两段表述(划线部分),你认为不能够支持“飞机仍是相对安全的交通工具”的所有表述序号为__________,你的理由是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]()
(1)求函数f(x)的解析式;
(2)若方程3[f(x)]2﹣f(x)+m=0在x∈( ![]() ,
, ![]() )内有两个不同的解,求实数m的取值范围.
)内有两个不同的解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com