
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),

(1)由图中数据求a的值;
(2)若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为多少?
(3)估计这所小学的小学生身高的众数,中位数(保留两位小数)及平均数.
【答案】(1)a=0.030;(2)3人;(3)众数115cm,中位数123.33cm,平均数124.5cm
【解析】
(1)根据频率和为1,求出[120,130)频率,再除以10,即为所求的值;
(2)先求出三组的人数,根据分层抽样按比例分配,将18人按比例分配,即可求解;
(3)根据直方图,频率最大组的中间值,为众数;从左到右求出频率和为0.5所在的组,再求出在该组所占的比例,即可求出中位数;根据平均数的公式,即可求解.
(1)因为直方图中的各个矩形的面积之和为1,
所以有10×(0.005+0.035+a+0.020+0.010)=1,
解得a=0.030;
(2)由直方图知,三个区域内的学生总数为
100×10×(0.030+0.020+0.010)=60人,
其中身高在[140,150]内的学生人数为10人,
所以从身高在[140,150]范围内抽取的学生人数为
![]() 10=3人;
10=3人;
(3)根据频率分布直方图知,身高在[110,120)内的小矩形图最高,
所以该组数据的众数为![]() 115cm;
115cm;
又0.005×10+0.035×10=0.4<0.5,
0.4+0.030×10=0.7>0.5,
所以中位数在[120,130)内,
则中位数为![]() ;
;
根据频率分布直方图,计算平均数为
105×0.05+115×0.35+125×0.3+135×0.2+145×0.1=124.5cm.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30人,则每人收取培训费1000元;若参加培训的员工人数超过30人,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算:公司此次培训的总费用最多需要多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即![]() .设函数
.设函数![]() ,二次函数
,二次函数![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,则
的图象有且只有一个公共点,则![]() 的取值不可能是( )
的取值不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题不正确的是( )
A.研究两个变量相关关系时,相关系数r为负数,说明两个变量线性负相关
B.研究两个变量相关关系时,相关指数R2越大,说明回归方程拟合效果越好.
C.命题“x∈R,cosx≤1”的否定命题为“x0∈R,cosx0>1”
D.实数a,b,a>b成立的一个充分不必要条件是a3>b3
查看答案和解析>>
科目:高中数学 来源: 题型:
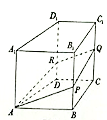
【题目】如图,在四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上一动点,过直线
上一动点,过直线![]() 的平面分别与棱
的平面分别与棱![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,则下列结论正确的是__________.
,则下列结论正确的是__________.
①对于任意的点![]() ,都有
,都有![]()
②对于任意的点![]() ,四边形
,四边形![]() 不可能为平行四边形
不可能为平行四边形
③存在点![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
④存在点![]() ,使得直线
,使得直线![]() 平面
平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com