
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的. 请根据4月7日,4月15日与4月21日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判定所得的线性回归方程是否可靠?
,并判定所得的线性回归方程是否可靠?
参考公式:  ,
, ![]()
参考数据: ![]()
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)用列举法列出所有的基本事件,分析可得“m,n均不小于25”的情况个数,用古典概型公式,计算即可得答案;(2)根据所给的数据,先做出![]() ,
, ![]() 的平均数,即做出本组数据的样本中心点,根据最小二乘法求出线性回归方程的系数,写出线性回归方程,再根据估计数据与所选出的检验数据的误差均不超过2颗,就认为得到的线性回归方程是可靠的,则根据求得的结果和所给的数据进行比较,即可得到所求的方程是可靠的.
的平均数,即做出本组数据的样本中心点,根据最小二乘法求出线性回归方程的系数,写出线性回归方程,再根据估计数据与所选出的检验数据的误差均不超过2颗,就认为得到的线性回归方程是可靠的,则根据求得的结果和所给的数据进行比较,即可得到所求的方程是可靠的.
试题解析:(1)所有的基本事件为(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),(30,26),(30,16),(26,16),共10个.
设“m,n均不小于25”为事件A,则事件A包含的基本事件为(25,30),(25,26),(30,26),共3个,故由古典概型概率公式得P(A)=![]() .
.
(2) 由题意得![]()
![]() 且
且![]() .
.
∴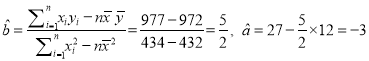 ,
,
∴![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,
,
且 当![]() 时,
时, ![]()
![]() ;
;
当![]() 时,
时, ![]()
![]() ;
;
当![]() 时,
时, ![]()
![]() ;
;
当![]() 时,
时, ![]()
![]() ;
;
当![]() 时,
时, ![]()
![]() .
.
∴所得到的线性回归方程是可靠的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165)、…、第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
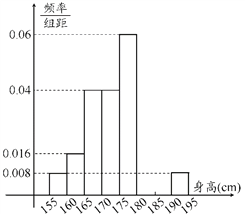
(2)求第六组、第七组的频率并补充完整频率分布直方图(如需增加刻度请在纵轴上标记出数据,并用直尺作图);
(3)由直方图估计男生身高的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于n∈N* , 若数列{xn}满足xn+1﹣xn>1,则称这个数列为“K数列”.
(Ⅰ)已知数列:1,m+1,m2是“K数列”,求实数m的取值范围;
(Ⅱ)是否存在首项为﹣1的等差数列{an}为“K数列”,且其前n项和Sn满足 ![]() ?若存在,求出{an}的通项公式;若不存在,请说明理由;
?若存在,求出{an}的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列{an}是“K数列”,数列 ![]() 不是“K数列”,若
不是“K数列”,若 ![]() ,试判断数列{bn}是否为“K数列”,并说明理由.
,试判断数列{bn}是否为“K数列”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点.如果函数
的不动点.如果函数
![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]()
(1)求函数![]() 的解析式;
的解析式;
(2)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(3)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起.设折起后点
折起.设折起后点![]() 的位置为
的位置为![]() ,并且平面
,并且平面![]()
![]() 平面
平面![]() .给出下面四个命题:
.给出下面四个命题:
①![]() ;②三棱锥
;②三棱锥![]() 的体积为
的体积为![]() ;③
;③![]()
![]() 平面
平面![]() ;
;
④平面![]() 平面
平面![]() .其中正确命题的序号是( )
.其中正确命题的序号是( )


A. ①② B. ③④ C. ①③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分). 
(1)求图中a的值;
(2)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(3)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(满分12分)学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(Ⅰ)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(Ⅱ)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式:![]() ,
,![]()
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在同一平面内,点P位于两平行直线l1、l2两侧,且P到l1 , l2的距离分别为1,3,点M,N分别在l1 , l2上,| ![]() +
+ ![]() |=8,则
|=8,则 ![]()
![]() 的最大值为( )
的最大值为( ) 
A.15
B.12
C.10
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com