
【题目】某企业为了了解该企业工人组装某产品所用时间,对每个工人组装一个该产品的用时作了记录,得到大量统计数据.从这些统计数据中随机抽取了![]() 个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过
个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过![]() (分钟),则称这个工人为优秀员工.
(分钟),则称这个工人为优秀员工.
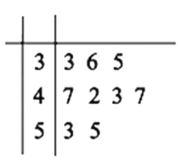
(1)求这个样本数据的中位数和众数;
(2)以这![]() 个样本数据中优秀员工的频率作为概率,任意调查
个样本数据中优秀员工的频率作为概率,任意调查![]() 名工人,求被调查的
名工人,求被调查的![]() 名工人中优秀员工的数量
名工人中优秀员工的数量![]() 分布列和数学期望.
分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
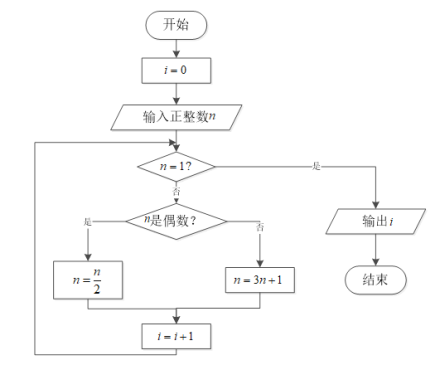
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s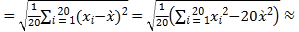 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求P(X=1)及/span>X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,以坐标原点
为参数,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线
轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设射线![]() 与曲线
与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,与曲线
,与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com