
【题目】已知函数![]() .
.
(1)若“![]() ,使得
,使得![]() ”为真命题,求
”为真命题,求![]() 的取值范围;
的取值范围;
(2)若不等式![]() 的解集为D,若
的解集为D,若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)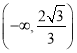 ;(2)
;(2)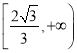 .
.
【解析】
(1)对![]() 分成
分成![]() 三种情况进行分类讨论,结合存在性问题,求解出
三种情况进行分类讨论,结合存在性问题,求解出![]() 的取值范围.
的取值范围.
(2)对![]() 分成
分成![]() 三种情况进行分类讨论,结合一元二次不等式的解法以及子集的知识,求得
三种情况进行分类讨论,结合一元二次不等式的解法以及子集的知识,求得![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,
,![]() ,使得
,使得![]() .
.
当![]() 时,二次函数
时,二次函数![]() 开口向下,
开口向下,![]() ,使得
,使得![]() .
.
当![]() 时,二次函数
时,二次函数![]() 开口向上,要使若“
开口向上,要使若“![]() ,使得
,使得![]() ”为真命题,则需其判别式
”为真命题,则需其判别式![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是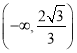
(2)当![]() 时,由
时,由![]() ,解得
,解得![]() ,所以
,所以![]() ,不满足
,不满足![]() .
.
当![]() 时,二次函数
时,二次函数![]() 开口向下,要使“不等式
开口向下,要使“不等式![]() 的解集为D,且
的解集为D,且![]() ”则需
”则需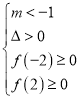 ,此不等式组无解.
,此不等式组无解.
当![]() 时,二次函数
时,二次函数![]() 开口向上,要使“不等式
开口向上,要使“不等式![]() 的解集为D,且
的解集为D,且![]() ”则需
”则需
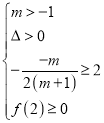 或
或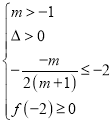 或
或![]() .
.
第一个不等式组的解集为空集,第二个不等式组的解集为空集,第三个不等式组的解集为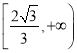 .
.
综上所述,![]() 的取值范围是
的取值范围是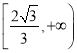 .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】自2019年春季以来,在非洲猪瘟、环保禁养、上行周期等因素形成的共振条件下,猪肉价格连续暴涨.某养猪企业为了抓住契机,决定扩大再生产,根据以往的养猪经验预估:在近期的一个养猪周期内,每养![]() 百头猪
百头猪![]() ,所需固定成本为20万元,其它为变动成本:每养1百头猪,需要成本14万元,根据市场预测,销售收入
,所需固定成本为20万元,其它为变动成本:每养1百头猪,需要成本14万元,根据市场预测,销售收入![]() (万元)与
(万元)与![]() (百头)满足如下的函数关系:
(百头)满足如下的函数关系:![]() (注:一个养猪周期内的总利润
(注:一个养猪周期内的总利润![]() (万元)=销售收入-固定成本-变动成本).
(万元)=销售收入-固定成本-变动成本).
(1)试把总利润![]() (万元)表示成变量
(万元)表示成变量![]() (百头)的函数;
(百头)的函数;
(2)当![]() (百头)为何值时,该企业所获得的利润最大,并求出最大利润.
(百头)为何值时,该企业所获得的利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是含数1的有限实数集,![]() 是定义在D上的函数.
是定义在D上的函数.
![]() 若
若![]() 的图象绕原点逆时针旋转
的图象绕原点逆时针旋转![]() 后与原图象重合,则
后与原图象重合,则![]() ______
______![]() 填是或否
填是或否![]() 可能为1.
可能为1.
![]() 若
若![]() 的图象绕原点逆时针旋转
的图象绕原点逆时针旋转![]() 后与原图象重合,则
后与原图象重合,则![]() 可能取值只能是______.
可能取值只能是______.
![]()
![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某火锅店为了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如表:

(1)求y关于x的回归方程![]() ;
;
(2)判定y与x之间是正相关还是负相关,若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的22列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]() .
.
附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”;
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”;
C.有99%以上的把握认为“爱好该项运动与性别有关”;
D.有99%以上的把握认为“爱好该项运动与性别无关”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查甲、乙两校高三年级学生某次联考数学成绩情况,现用简单随机抽样从这两个学校高三年级学生中各抽取30名,以他们的数学成绩(百分制)作为样本,样本数据如下.

(1)若甲校高三年级每位学生被抽到的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);
(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为![]() ,
,![]() ,估计
,估计![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com