
 .
.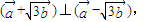 整理可求Q点的轨迹方程.
整理可求Q点的轨迹方程.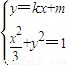 得(3k2+1)x2+6mkx+3(m2-1)=0,结合直线与椭圆有两个不同的交点,可得△>0,从而可得m与k得关系,设弦MN的中点为P由|AM|=|AN|,可得AP⊥MN,从而有KAP•Kmn=-1,代入可求.
得(3k2+1)x2+6mkx+3(m2-1)=0,结合直线与椭圆有两个不同的交点,可得△>0,从而可得m与k得关系,设弦MN的中点为P由|AM|=|AN|,可得AP⊥MN,从而有KAP•Kmn=-1,代入可求. ,∵
,∵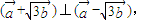 .∴
.∴ …(4分)
…(4分)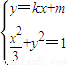 得(3k2+1)x2+6mkx+3(m2-1)=0,
得(3k2+1)x2+6mkx+3(m2-1)=0,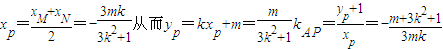 …(8分)
…(8分)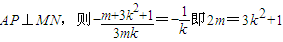 ②,将②代入①得2m>m2,解得0<m<2,由②得
②,将②代入①得2m>m2,解得0<m<2,由②得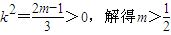 ,故所求的m取值范围是
,故所求的m取值范围是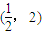 .…(10分)
.…(10分) …(12分)
…(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
在平面直角坐标系中,已知向量![]() (
(![]() ),
),![]() ,动点
,动点![]() 的轨迹为T.
的轨迹为T.
(1)求轨迹T的方程,并说明该方程表示的曲线的形状;
(2)当![]() 时,已知
时,已知![]() 、
、![]() ,试探究是否存在这样的点
,试探究是否存在这样的点![]() :
: ![]() 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积![]() ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:广东省揭阳市2010年高考一模(文) 题型:解答题
(本题满分14分)
在平面直角坐标系中,已知向量 (
( ),
), ,动点
,动点 的轨迹为T.
的轨迹为T.
(1)求轨迹T的方程,并说明该方程表示的曲线的形状;
(2)当 时,已知
时,已知 、
、 ,试探究是否存在这样的点
,试探究是否存在这样的点 :
: 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省山一中高三热身练文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
在平面直角坐标系中,已知向量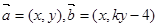 (
(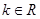 ),
),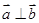 ,动点
,动点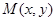 的轨迹为
的轨迹为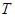 .
.
(1)求轨迹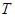 的方程,并说明该方程表示的曲线的形状;
的方程,并说明该方程表示的曲线的形状;
(2)当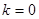 时,过点
时,过点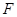 (0,1),作轨迹T的两条互相垂直的弦
(0,1),作轨迹T的两条互相垂直的弦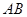 、
、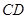 ,设
,设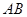 、
、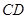 的中点分别为
的中点分别为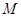 、
、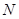 ,试判断直线
,试判断直线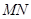 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com