
 ,问其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003600≈6,e≈2.70828…,e8≈2981)
,问其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003600≈6,e≈2.70828…,e8≈2981) lnx+1,易知满足①,当x∈[10,1000]时时,y≤
lnx+1,易知满足①,当x∈[10,1000]时时,y≤ ln1000+1…(7分)
ln1000+1…(7分) ln1000+1<5.
ln1000+1<5. ln1000+1-5=
ln1000+1-5= ln1000-4=
ln1000-4= (ln1000-8)=
(ln1000-8)= (ln1000-ln2981)<0,满足②…(8分)
(ln1000-ln2981)<0,满足②…(8分) lnx+1≤x•25%,即2lnx+4-x≤0,…(9分)
lnx+1≤x•25%,即2lnx+4-x≤0,…(9分) -1=
-1= <0,x∈[10,1000]…(10分)
<0,x∈[10,1000]…(10分) lnx+1能完全符合公司的要求…(13分)
lnx+1能完全符合公司的要求…(13分) lnx+1三个函数逐一分析即可.
lnx+1三个函数逐一分析即可.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省临沂市临沭县高三(上)期中数学试卷(理科)(解析版) 题型:解答题
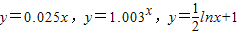 ,问其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003600≈6,e≈2.70828…,e8≈2981)
,问其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003600≈6,e≈2.70828…,e8≈2981)查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省临沂市高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 ,问其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003600≈6,e≈2.70828…,e8≈2981)
,问其中是否有模型能完全符合公司的要求?请说明理由.(参考数据:1.003600≈6,e≈2.70828…,e8≈2981)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com