
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 在①中,由线面垂直的判定定理得n⊥α;在②中,m与n相交、平行或异面;在③中,m与n相交、平行或异面;在④中,由线面垂直的判定定理得m⊥β.
解答 解:由两个不同的平面α、β和两个不重合的直线m、n,知:
在①中,若m∥n,m⊥α,则由线面垂直的判定定理得n⊥α,故①正确;
在②中,若m∥α,α∩β=n,则m与n相交、平行或异面,故②错误;
在③中,若m⊥α,α⊥β,n?β,则m与n相交、平行或异面,故③错误;
在④中,若m⊥α,α∥β,则由线面垂直的判定定理得m⊥β,故④正确.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


科目:高中数学 来源: 题型:选择题
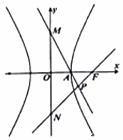 如图,双曲线的中心在坐标原点O,M、N分别为双曲线虚轴的上、下端点,A是双曲线的右顶点,F是双曲线的右焦点,直线AM与FN相交于点P,若∠APF是锐角,则此双曲线的离心率的取值范围是( )
如图,双曲线的中心在坐标原点O,M、N分别为双曲线虚轴的上、下端点,A是双曲线的右顶点,F是双曲线的右焦点,直线AM与FN相交于点P,若∠APF是锐角,则此双曲线的离心率的取值范围是( )| A. | ($\frac{1+\sqrt{5}}{2}$,+∞) | B. | (1+$\sqrt{5}$,+∞) | C. | (0,$\frac{\sqrt{5}-1}{2}$) | D. | ($\frac{1+\sqrt{5}}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左移动$\frac{1}{2}$个单位 | B. | 向右移动$\frac{1}{2}$个单位 | ||
| C. | 向左移动1个单位 | D. | 向右移动1个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 钝角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC为直径的球面交PD于M点.
在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC为直径的球面交PD于M点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com