12
分析:由
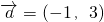
,
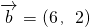
,先分别求出

和
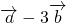
,再由向量

与
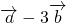
垂直,知(

)•(
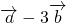
)=0,由此能求出实数λ.
解答:∵
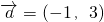
,
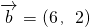
,
∴

=(-λ+6,3λ+2),
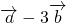
=(-19,-3),
∵向量

与
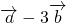
垂直,
∴(

)•(
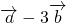
)=-19(-λ+6)-3(3λ+2)=0,
解得λ=12.
故答案为:12.
点评:本题考查数量积判断两个平面向量的垂直关系的应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.
练习册系列答案
相关习题
科目:高中数学
来源:2011-2012学年上海浦东高三第六次联考理科数学
题型:填空题
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省济宁市鱼台一中高三(上)期末数学模拟试卷(理科)(解析版)
题型:选择题
已知
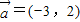
,
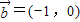
,向量
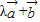
与
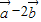
垂直,则实数λ的值为( )
A.-

B.

C.-

D.

查看答案和解析>>
科目:高中数学
来源:2009-2010学年北京四中高一(上)期末数学试卷(解析版)
题型:选择题
已知
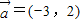
,
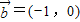
,向量
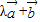
与
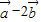
垂直,则实数λ的值为( )
A.-

B.

C.-

D.

查看答案和解析>>
科目:高中数学
来源:2013年广东省梅州市高考数学二模试卷(理科)(解析版)
题型:选择题
已知
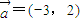
,
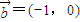
,向量
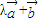
与
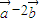
垂直,则实数λ的值为( )
A.-

B.

C.-

D.

查看答案和解析>>
科目:高中数学
来源:2013年河南省新乡、许昌、平顶山高考数学一模试卷(文科)(解析版)
题型:选择题
已知
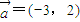
,
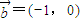
,向量
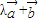
与
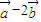
垂直,则实数λ的值为( )
A.-

B.

C.-

D.

查看答案和解析>>

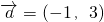 ,
,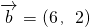 ,向量
,向量 与
与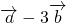 垂直,则实数λ=________.
垂直,则实数λ=________.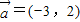 ,
,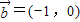 ,向量
,向量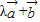 与
与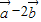 垂直,则实数λ的值为( )
垂直,则实数λ的值为( )


