
،¾جâؤ؟،؟ز»¸ِ¹¤³§ةْ²ْؤ³ضض²ْئ·أ؟ؤêذèزھ¹ج¶¨ح¶×ت100حٍشھ,´ثحâأ؟ةْ²ْ1¼¸أ²ْئ·»¹ذèزھشِ¼سح¶×ت1حٍشھ,ؤê²ْء؟خھ![]() £¨
£¨![]() £©¼.µ±
£©¼.µ±![]() ت±£¬ؤêدْتغ×ـتصبثخھ£¨
ت±£¬ؤêدْتغ×ـتصبثخھ£¨![]() £©حٍشھ£»µ±
£©حٍشھ£»µ±![]() ت±£¬ؤêدْتغ×ـتصبثخھ
ت±£¬ؤêدْتغ×ـتصبثخھ![]() حٍشھ.¼ا¸أ¹¤³§ةْ²ْ²¢دْتغصâضض²ْئ·ثùµأµؤؤêہûبَخھ
حٍشھ.¼ا¸أ¹¤³§ةْ²ْ²¢دْتغصâضض²ْئ·ثùµأµؤؤêہûبَخھ![]() حٍشھ.(ؤêہûبَ=ؤêدْتغ×ـتصبëز»ؤê×ـح¶×ت)
حٍشھ.(ؤêہûبَ=ؤêدْتغ×ـتصبëز»ؤê×ـح¶×ت)
(1)اَ![]() (حٍشھ)سë
(حٍشھ)سë![]() (¼)µؤ؛¯ت¹طدµت½£»
(¼)µؤ؛¯ت¹طدµت½£»
(2)µ±¸أ¹¤³§µؤؤê²ْء؟خھ¶àةظ¼ت±,ثùµأؤêہûبَ×î´َ?×î´َؤêہûبَتا¶àةظ?
،¾´ً°¸،؟£¨1£©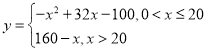 £¨
£¨![]() £©£»£¨2£©µ±ؤê²ْء؟خھ
£©£»£¨2£©µ±ؤê²ْء؟خھ![]() ¼ت±£¬ثùµأؤêہûبَ×î´َ£¬×î´َؤêہûبَخھ
¼ت±£¬ثùµأؤêہûبَ×î´َ£¬×î´َؤêہûبَخھ![]() حٍشھ.
حٍشھ.
،¾½âخِ،؟
£¨1£©¸ù¾فزرضھجُ¼£¬·ضµ±![]() ت±؛حµ±
ت±؛حµ±![]() ت±ء½ضضاé؟ِ£¬·ض±ًاَ³ِؤêہûبَµؤ±ي´ïت½£¬×غ؛د؟ةµأ´ً°¸£»
ت±ء½ضضاé؟ِ£¬·ض±ًاَ³ِؤêہûبَµؤ±ي´ïت½£¬×غ؛د؟ةµأ´ً°¸£»
£¨2£©¸ù¾ف£¨1£©ضذ؛¯تµؤ½âخِت½£¬اَ³ِ×î´َضµµم؛ح×î´َضµ¼´؟ة£®
£¨1£©سةجâزâµأ£؛µ±![]() ت±£¬
ت±£¬![]() £¬
£¬
µ±![]() ت±£¬
ت±£¬![]() £¬
£¬
¹ت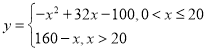 £¨
£¨![]() £©£»
£©£»
£¨2£©µ±![]() ت±£¬
ت±£¬![]() £¬
£¬
µ±![]() ت±£¬
ت±£¬![]() £¬
£¬
¶ّµ±![]() ت±£¬
ت±£¬![]() £¬
£¬
¹تµ±ؤê²ْء؟خھ![]() ¼ت±£¬ثùµأؤêہûبَ×î´َ£¬×î´َؤêہûبَخھ
¼ت±£¬ثùµأؤêہûبَ×î´َ£¬×î´َؤêہûبَخھ![]() حٍشھ.
حٍشھ.



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟[2018،¤¸سضذءھ؟¼]ہîز±£¨1192-1279£©£¬صوتµèï³ا£¨½ٌتô؛س±±ت¯¼زׯتذ£©بث£¬½ًشھت±ئعµؤتر§¼ز،¢ت«بث£¬حيؤêشع·âءْة½ز¾س½²ر§£¬تر§ضّ×÷¶à²؟£¬ئنضذ،¶زو¹إرف¶خ،·ض÷زھرذ¾؟ئ½أوح¼ذخختجâ£؛اَش²µؤض±¾¶،¢ص·½ذخµؤ±ك³¤µب£®ئنضذز»خت£؛دضسذص·½ذخ·½جïز»؟飬ؤع²؟سذز»¸ِش²ذخث®³ط£¬ئنضذث®³طµؤ±كشµسë·½جïثؤ±كض®¼نµؤأو»خھ13.75ؤ¶£¬بô·½جïµؤثؤ±كµ½ث®³طµؤ×î½ü¾àہë¾ùخھ¶ت®²½£¬شٍش²³طض±¾¶؛ح·½جïµؤ±ك³¤·ض±ًتا£¨×¢£؛240ئ½·½²½خھ1ؤ¶£¬ش²ضـآت°´3½üثئ¼ئثم£©£¨ £©
A. 10²½£¬50²½ B. 20²½£¬60²½ C. 30²½£¬70²½ D. 40²½£¬80²½
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ؛¯ت![]() £¨ئنضذ
£¨ئنضذ![]() خھ³£ت£©
خھ³£ت£©
£¨1£©اَ![]() µؤµ¥µ÷شِاّ¼ن£»
µؤµ¥µ÷شِاّ¼ن£»
£¨2£©بô![]() ت±£¬
ت±£¬![]() µؤ×î´َضµخھ
µؤ×î´َضµخھ![]() £¬اَ
£¬اَ![]() µؤضµ£»
µؤضµ£»
£¨3£©اَ![]() ب،×î´َضµت±
ب،×î´َضµت±![]() µؤب،ضµ¼¯؛د.
µؤب،ضµ¼¯؛د.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھدآءذثؤ¸ِأüجâ:
¢ظ؛¯ت![]() آْ×م:¶شبخزâ
آْ×م:¶شبخزâ![]() سذ
سذ![]() £»
£»
¢ع؛¯ت![]() ¾ùخھئو؛¯ت£»
¾ùخھئو؛¯ت£»
¢غبô؛¯ت![]() شع
شع![]() ةدسذزâزه£¬شٍ
ةدسذزâزه£¬شٍ![]() µؤب،ضµ·¶خ§تا
µؤب،ضµ·¶خ§تا![]() £»
£»
¢ـةè![]() تا¹طسع
تا¹طسع![]() µؤ·½³ج
µؤ·½³ج![]() ,(
,(![]() از
از![]() )µؤء½¸ù,شٍ
)µؤء½¸ù,شٍ![]() ;
;
ئنضذصب·أüجâµؤذٍ؛إتا__________£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
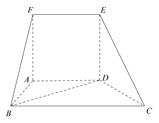
،¾جâؤ؟،؟بçح¼£¬شع¶àأوجه![]() ضذ£¬ئ½أو
ضذ£¬ئ½أو![]() ئ½أو
ئ½أو![]() £¬ثؤ±كذخ
£¬ثؤ±كذخ![]() خھص·½ذخ£¬ثؤ±كذخ
خھص·½ذخ£¬ثؤ±كذخ![]() خھجفذخ£¬از
خھجفذخ£¬از![]() £¬
£¬![]() £¬
£¬![]() £®
£®
£¨1£©اَض¤£؛![]() ئ½أو
ئ½أو![]() £»
£»
£¨2£©شعدك¶خ![]() ةدتا·ٌ´وشعµم
ةدتا·ٌ´وشعµم![]() £¬ت¹µأ
£¬ت¹µأ![]() ئ½أو
ئ½أو![]() £؟بô´وشع£¬اَ³ِ
£؟بô´وشع£¬اَ³ِ![]() µؤضµ£»بô²»´وشع£¬اëثµأ÷ہيسة.
µؤضµ£»بô²»´وشع£¬اëثµأ÷ہيسة.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ![]() خھإ¼؛¯ت£®
خھإ¼؛¯ت£®
£¨1£©اَتµت![]() µؤضµ£¬²¢ذ´³ِ
µؤضµ£¬²¢ذ´³ِ![]() شعاّ¼ن
شعاّ¼ن![]() ةدµؤشِ¼ُذش؛حضµسٍ£¨²»ذèزھض¤أ÷£©£»
ةدµؤشِ¼ُذش؛حضµسٍ£¨²»ذèزھض¤أ÷£©£»
£¨2£©ءî![]() £¬ئنضذ
£¬ئنضذ![]() £¬بô
£¬بô![]() ¶شبخزâ
¶شبخزâ![]() ،¢
،¢![]() £¬×ـسذ
£¬×ـسذ![]() £¬اَ
£¬اَ![]() µؤب،ضµ·¶خ§£»
µؤب،ضµ·¶خ§£»
£¨3£©ءî![]() £¬بô
£¬بô![]() ¶شبخزâ
¶شبخزâ![]() ،¢
،¢![]() £¬×ـسذ
£¬×ـسذ![]() £¬اَتµت
£¬اَتµت![]() µؤب،ضµ·¶خ§£®
µؤب،ضµ·¶خ§£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھ؛¯ت![]()
£¨1£©اَ؛¯ت![]() µؤ×îذ،صضـئع،¢µ¥µ÷اّ¼ن£»
µؤ×îذ،صضـئع،¢µ¥µ÷اّ¼ن£»
£¨2£©اَ؛¯ت![]() شعاّ¼ن
شعاّ¼ن![]() ةدµؤ×îذ،ضµ؛ح×î´َضµ.
ةدµؤ×îذ،ضµ؛ح×î´َضµ.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼ثùت¾£¬بہâضùABC©پA1B1C1ضذ£¬²àہâAA1،حµ×أوA1B1C1£¬AA1£½1£¬µ×أوب½اذخA1B1C1تا±ك³¤خھ2µؤصب½اذخ£¬EتاBCضذµم£¬شٍدآءذثµ·¨صب·µؤتا£¨ £©

¢ظCC1سëAB1ثù³ة½اµؤسàدزضµخھ![]()
¢عAB،حئ½أوACC1A1
¢غب½اذخAB1Eخھض±½اب½اذخ
¢ـA1C1،خئ½أوAB1E
A.¢ظ¢عB.¢غ¢ـC.¢ظ¢غD.¢ع¢ـ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛¸كضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟5أûؤذةْ3أûإ®ةْ²خ¼سةئىزات½£؛
£¨1£©ص¾ء½؛لإإ£¬3أûإ®ةْص¾ا°إإ£¬5أûؤذةْص¾؛َإإسذ¶àةظضضص¾·¨£؟
£¨2£©ص¾ء½×فءذ£¬أ؟ءذ4بث£¬أ؟ءذ¶¼سذإ®ةْازإ®ةْص¾شعؤذةْا°أو£¬سذ¶àةظضضإإءذ·½·¨£؟
²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com