
【题目】下列几个命题:①若方程![]() 的两个根异号,则实数
的两个根异号,则实数![]() ;②函数
;②函数![]() 是偶函数,但不是奇函数;③函数
是偶函数,但不是奇函数;③函数 ![]() 在
在![]() 上是减函数,则实数a的取值范围是
上是减函数,则实数a的取值范围是![]() ;④ 方程
;④ 方程 ![]() 的根
的根![]() 满足
满足![]() ,则m满足的范围
,则m满足的范围![]() ,其中不正确的是( )
,其中不正确的是( )
A.①B.②C.③D.④
科目:高中数学 来源: 题型:
【题目】已知一元二次函数f(x)=ax2+bx+c(a>0,c>0)的图象与x轴有两个不同的公共点,其中一个公共点的坐标为(c,0),且当0<x<c时,恒有f(x)>0.
(1)当a=1,![]() 时,求出不等式f(x)<0的解;
时,求出不等式f(x)<0的解;
(2)求出不等式f(x)<0的解(用a,c表示);
(3)若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD,底面ABCD为菱形,且∠DAB=60°,△PAB是边长为a的正三角形,且平面PAB⊥平面ABCD,已知点M是PD的中点.
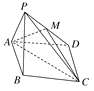
(1)证明:PB∥平面AMC;
(2)求直线BD与平面AMC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
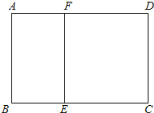
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后掷一颗质地均匀的骰子(骰子的六个面上分别标有1,2,3,4,5,6)两次,落在水平桌面上后,记正面朝上的点数分别为![]() ,记事件
,记事件![]() 为“
为“![]() 为偶数”,事件
为偶数”,事件![]() 为“
为“![]() 中有偶数且
中有偶数且![]() ”,则概率
”,则概率![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足下列3个条件:①函数
满足下列3个条件:①函数![]() 的图象过坐标原点; ②函数
的图象过坐标原点; ②函数![]() 的对称轴方程为
的对称轴方程为![]() ; ③方程
; ③方程![]() 有两个相等的实数根.
有两个相等的实数根.
(1)求函数![]() 的解析式;
的解析式;
(2)令![]() ,若函数
,若函数![]() 在
在![]() 上的最小值为-3,求实数
上的最小值为-3,求实数![]() 的值;
的值;
(3)令![]() ,若函数
,若函数![]() 在
在![]() 内有零点,求实数
内有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且抛物线
,且抛物线![]() 的焦点恰好是椭圆
的焦点恰好是椭圆![]() 的一个焦点.
的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() (
(![]() 为坐标原点),求四边形
为坐标原点),求四边形![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员每次射击命中不低于8环的概率为![]() ,命中8环以下的概率为
,命中8环以下的概率为![]() ,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先由计算器产生0到9之间取整数值的随机数,指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以每三个随机数为一组,代表三次射击的结果,产生了如下20组随机数:
,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先由计算器产生0到9之间取整数值的随机数,指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以每三个随机数为一组,代表三次射击的结果,产生了如下20组随机数:
![]()
据此估计,该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,曲线
为奇函数,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,导函数
垂直,导函数![]() 的最小值为-12.
的最小值为-12.
(1)求函数![]() 的解析式;
的解析式;
(2)用列表法求函数![]() 在
在![]() 上的单调增区间、极值、最值.
上的单调增区间、极值、最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com