
【题目】设集合![]() 表示具有下列性质的函数
表示具有下列性质的函数![]() 的集合:①
的集合:①![]() 的定义域为
的定义域为![]() ;②对任意
;②对任意![]() ,都有
,都有![]()
(1)若函数![]() ,证明
,证明![]() 是奇函数;并当
是奇函数;并当![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)设函数![]() (a为常数)是奇函数,判断
(a为常数)是奇函数,判断![]() 是否属于
是否属于![]() ,并说明理由;
,并说明理由;
(3)在(2)的条件下,若 ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)见解析,![]() ,
,![]()
(2)![]() ,证明见解析
,证明见解析
(3)![]() 或
或![]() 时,3个零点;
时,3个零点;![]() 或
或![]() 时,1个零点;
时,1个零点;![]() 时,5个零点.
时,5个零点.
【解析】
(1)利用赋值法和奇函数的定义证明函数是奇函数,由题得![]() 的方程组,解方程组即得解;(2)先求出a的值,再利用
的方程组,解方程组即得解;(2)先求出a的值,再利用![]() 的定义证明;(3)令h(x)=t,则h(t)=2,再分类讨论数形结合分析得解.
的定义证明;(3)令h(x)=t,则h(t)=2,再分类讨论数形结合分析得解.
(1)令![]() 得
得![]() .
.
令![]() ,
,![]() ,所以函数
,所以函数![]() 是奇函数.
是奇函数.
![]() ,
,![]()
解上面关于![]() 的方程组得
的方程组得![]() ,
,![]() .
.
(2)因为函数![]() (a为常数)是奇函数,
(a为常数)是奇函数,
所以![]() .满足函数g(x)是奇函数.
.满足函数g(x)是奇函数.
设![]() ,所以
,所以![]() ,
,
因为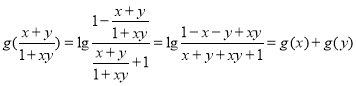 ,
,
所以![]() .
.
(3)令![]() .
.
令h(x)=t,则h(t)=2,
所以函数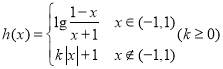
当k=0时,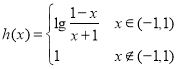 ,则
,则![]() ,此时只有一个解,一个零点;
,此时只有一个解,一个零点;
当![]() 时,只有一个
时,只有一个![]() ,对应三个零点;
,对应三个零点;
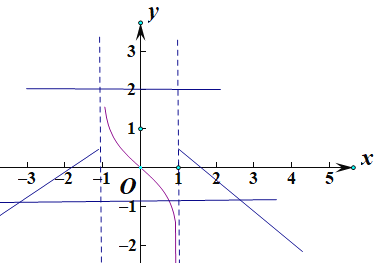
当![]() 时,
时,![]() ,此时
,此时![]() ,
,
![]() ,
,
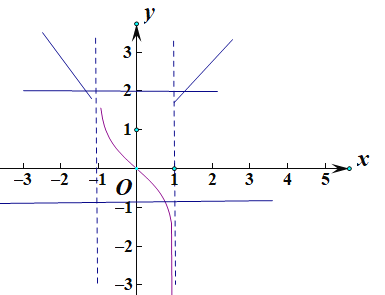
所以在![]() ,
,![]() ,三个t各对应一个零点,共三个零点;
,三个t各对应一个零点,共三个零点;
当![]() ,
,![]() ,三个t各对应一个,一个,三个零点,共五个零点;
,三个t各对应一个,一个,三个零点,共五个零点;
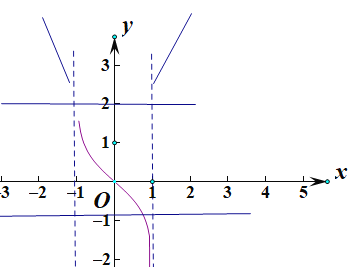
当![]() 时,h(t)=2只有一个解,
时,h(t)=2只有一个解,![]() ,对应一个零点.
,对应一个零点.
综合得![]() 或
或![]() 时,3个零点;
时,3个零点;![]() 或
或![]() 时,1个零点;
时,1个零点;![]() 时,5个零点.
时,5个零点.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
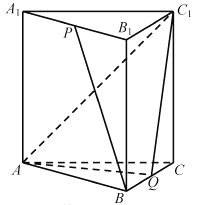
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
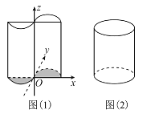
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图(1),函数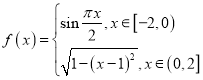 的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域是一切实数的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() (
(![]() )使得
)使得![]() 对任意实数
对任意实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() -伴随函数”,有下列关于“
-伴随函数”,有下列关于“![]() -伴随函数”的结论:①
-伴随函数”的结论:①![]() 是常数函数唯一一个“
是常数函数唯一一个“![]() -伴随函数”;②“
-伴随函数”;②“![]() -伴随函数”至少有一个零点;③
-伴随函数”至少有一个零点;③![]() 是一个“
是一个“![]() -伴随函数”;其中正确结论的个数( )
-伴随函数”;其中正确结论的个数( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同的直线,![]() ,
,![]() 是两个不同的平面,给出下列命题:
是两个不同的平面,给出下列命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,则
,则![]() 或
或![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() 或
或![]() ;
;
④若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 且
且![]() ;
;
其中正确命题的序号是( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
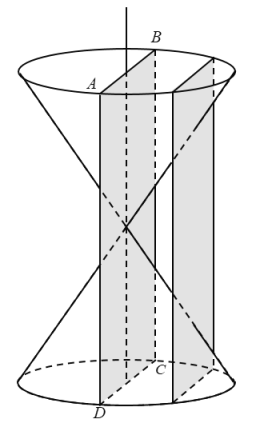
【题目】古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面切制圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径为1,母线长均为![]() ,记过圆锥轴的平面ABCD为平面
,记过圆锥轴的平面ABCD为平面![]() (
(![]() 与两个圆锥面的交线为AC、BD),用平行于
与两个圆锥面的交线为AC、BD),用平行于![]() 的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某中学高三年级利用课余时间组织学生开展小型知识竞赛.比赛规则:每个参赛者回答A、B两组题目,每组题目各有两道题,每道题答对得1分,答错得0分,两组题目得分的和做为该选手的比赛成绩.小明估计答对A组每道题的概率均为![]() ,答对B组每道题的概率均为
,答对B组每道题的概率均为![]() .
.
(Ⅰ)按此估计求小明A组题得分比B组题得分多1分的概率;
(Ⅱ)记小明在比赛中的得分为ξ,按此估计ξ的分布列和数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com