
【题目】甲、乙、丙、丁四个人到![]() ,
,![]() ,
,![]() 三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到
三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到![]() 景点的方案有( )
景点的方案有( )
A.18种B.12种C.36种D.24种
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
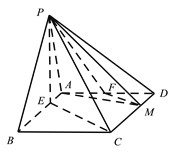
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:其中所有假命题的序号是_______.
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ;
;
②将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像;
的图像;
③幂函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() ;
;
④函数![]() 有两个零点.
有两个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和到直线
和到直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点作垂直于
,过点作垂直于![]() 轴的直线与曲线
轴的直线与曲线![]() 相交于两点,直线
相交于两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 相交于一点(交点位于线段
相交于一点(交点位于线段![]() 上,且与
上,且与![]() 不重合).
不重合).
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,四边形
相切时,四边形![]() 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】因客流量临时增大,某鞋店拟用一个高为50![]() (即
(即![]() )的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客
)的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客![]() 的眼睛
的眼睛![]() 到地面的距离为
到地面的距离为![]() (
(![]() )在区间
)在区间![]() 内,设支架
内,设支架![]() 高为
高为![]() (
(![]() )
)![]() ,
,![]() ,顾客可视的镜像范围为
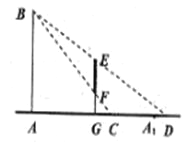
,顾客可视的镜像范围为![]() (如图所示),记
(如图所示),记![]() 的长度为
的长度为![]() (
(![]() ).
).
(I)当![]() 时,试求
时,试求![]() 关于
关于![]() 的函数关系式和
的函数关系式和![]() 的最大值;
的最大值;
(II)当顾客的鞋![]() 在镜中的像
在镜中的像![]() 满足不等关系
满足不等关系![]() (不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求
(不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 与点
与点![]() 均在椭圆
均在椭圆![]() 上,且
上,且![]() 关于原点对称,问:椭圆上是否存在点
关于原点对称,问:椭圆上是否存在点![]() (点
(点![]() 在一象限),使得
在一象限),使得![]() 为等边三角形?若存在,求出点
为等边三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com