
【题目】为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物释放过程中,室内每立方米空气中的含药量![]() 与时间
与时间![]() 成正比,药物释放完毕后,
成正比,药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数).如图所示,根据图中提供的信息,回答下列问题:
为常数).如图所示,根据图中提供的信息,回答下列问题:
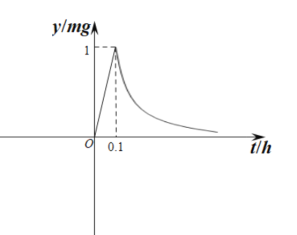
(1)从药物释放开始,每立方米空气中的含药量![]() 与时间
与时间![]() 之间的函数关系式为________;
之间的函数关系式为________;
(2)据测定,当空气中每立方米的含药量降低到![]() 以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
以下时,学生方可进教室,那么从药物释放开始,至少需要经过多少时间学生才能回到教室?
 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中,![]() ,若
,若![]() (
(![]() 为常数),则称
为常数),则称![]() 为“等差比数列”.下列是对“等差比数列”的判断:
为“等差比数列”.下列是对“等差比数列”的判断:
①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列;
;②等差数列一定是等差比数列;
③等比数列一定是等差比数列;④等差比数列中可以有无数项为![]() .
.
其中正确的判断是( ).
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(1)求抛物线M的方程;
(2)过点F斜率为k的直线l与M相交于C,D两点,线段![]() 的垂直平分线
的垂直平分线![]() 与M相交于
与M相交于![]() 两点,点
两点,点![]() 分别为线段
分别为线段![]() 和
和![]() 的中点.
的中点.
①试用k表示点![]() 的坐标;
的坐标;
②若以线段![]() 为直径的圆过点C,求直线l的方程.
为直径的圆过点C,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年2月份,我国武汉地区爆发了新冠肺炎疫情,为了预防疫情蔓延,全国各大医药厂商纷纷加紧生产口罩,某医疗器械生产工厂为了解目前的生产力,统计了每个工人每小时生产的口罩数量(单位:箱),得到如图所示的频率分布直方图,其中每个工人每小时的产量均落在[10,70]内,数据分组为[10,20)、[20,30)、[30,40)、[40,50)、[50,60)、![]() ,已知前三组的频率成等差数列,第三组、第四组、第五组的频率成等比数列,最后一组的频率为
,已知前三组的频率成等差数列,第三组、第四组、第五组的频率成等比数列,最后一组的频率为![]() .
.
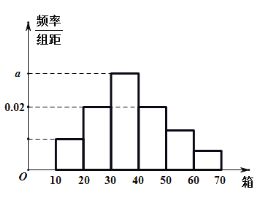
(1)求实数a的值;
(2)在最后三组中采用分层抽样的方法随机抽取了6人,现从这6人中随机抽出两人对其它小组的工人进行生产指导,求这两人来自同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,其前n项的积为
的各项均为正数,其前n项的积为![]() ,记
,记![]() ,
,![]() .
.
(1)若数列![]() 为等比数列,数列
为等比数列,数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求数列![]() 的通项公式.
的通项公式.
②记![]() ,那么数列
,那么数列![]() 中是否存在两项
中是否存在两项![]() ,(s,t均为正偶数,且
,(s,t均为正偶数,且![]() ),使得数列
),使得数列![]() ,
,![]() ,
,![]() ,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为坐标原点O,对称轴为![]() 轴,其准线为
轴,其准线为![]() .
.
(1)求抛物线C的方程;
(2)设直线![]() ,对任意的
,对任意的![]() 抛物线C上都存在四个点到直线l的距离为
抛物线C上都存在四个点到直线l的距离为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() ,
,![]() ,给出以下四种排序:①M,N,T;②M,T,N;③N,T,M;④T,N,M.从中任选一个,补充在下面的问题中,解答相应的问题.
,给出以下四种排序:①M,N,T;②M,T,N;③N,T,M;④T,N,M.从中任选一个,补充在下面的问题中,解答相应的问题.
已知等比数列![]() 中的各项都为正数,
中的各项都为正数,![]() ,且__________依次成等差数列.
,且__________依次成等差数列.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设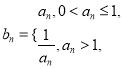 数列
数列![]() 的前n项和为
的前n项和为![]() ,求满足
,求满足![]() 的最小正整数n.
的最小正整数n.
注:若选择多种排序分别解答,按第一个解答计分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com