
【题目】已知函数![]() .
.
(Ⅰ)判断函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(Ⅱ)若函数![]() 在区间
在区间![]() 上满足
上满足![]() 恒成立,求实数a的最小值.
恒成立,求实数a的最小值.
【答案】(1) 单调递减.(2)1
【解析】试题分析:(1)先求导数得![]() ,再研究
,再研究![]() ,得
,得![]() 在区间
在区间![]() 上恒小于零,可得
上恒小于零,可得![]() 在区间
在区间![]() 上恒小于零,即得函数单调性(2)由不等式恒成立得
上恒小于零,即得函数单调性(2)由不等式恒成立得![]() ,再利用洛必达法则求
,再利用洛必达法则求![]() ,即得
,即得![]() ,可得实数a的最小值.
,可得实数a的最小值.
试题解析:解:(Ⅰ)当![]() 时,
时, ![]()
令![]() ,
, ![]() ,显然当
,显然当![]() 时,
时,
![]() ,即函数
,即函数![]() 在区间
在区间![]() 的单调递减,且
的单调递减,且![]() ,
,
从而函数![]() 在区间
在区间![]() 上恒小于零
上恒小于零
所以![]() 在区间
在区间![]() 上恒小于零,函数
上恒小于零,函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
(Ⅱ)由于![]() ,不等式
,不等式![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
令![]() ,
, ![]() ,且
,且![]()
当![]() 时,在区间
时,在区间![]() 上
上![]() ,即函数
,即函数![]() 单调递减,
单调递减,
所以![]() ,即
,即![]() 恒成立
恒成立
当![]() 时,
时, ![]() 在区间
在区间![]() 上存在唯一解
上存在唯一解![]() ,
,
当![]() 时,
时, ![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,且
上单调递增,且![]() ,
,
从而![]() 在区间
在区间![]() 上大于零,这与
上大于零,这与![]() 恒成立相矛盾 当
恒成立相矛盾 当![]() 时,在区间
时,在区间![]() 上
上![]() ,即函数
,即函数![]() 单调递增,且
单调递增,且![]() ,
,
得![]() 恒成立,这与
恒成立,这与![]() 恒成立相矛盾
恒成立相矛盾
故实数a的最小值为1.


科目:高中数学 来源: 题型:
【题目】某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )
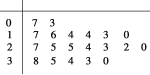

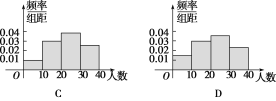
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数M,使得函数
,存在一个正数M,使得函数![]() 的值域包含于区间[-M,M]。例如,当
的值域包含于区间[-M,M]。例如,当![]() ,
, ![]() 时,
时, ![]() ,现有如下命题:
,现有如下命题:
①设函数![]() 的定义域为D,则“
的定义域为D,则“![]() ”的充要条件是“
”的充要条件是“![]() ”;
”;
②若函数![]() ,则
,则![]() 有最大值和最小值;
有最大值和最小值;
③若函数![]() ,
, ![]() 的定义域相同,且
的定义域相同,且![]() ,
, ![]() ,则
,则![]()
④若函数![]() ,则
,则![]() 有最大值且
有最大值且![]() ,
,
其中的真命题有_____________。(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙,丙,丁四名同学做传递手帕游戏(每位同学传递到另一位同学记传递1次),手帕从甲手中开始传递,经过5次传递后手帕回到甲手中,则共有__________种不同的传递方法.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为减少汽车尾气排放,提高空气质量,各地纷纷推出汽车尾号限行措施.为做好此项工作,某市交警支队对市区各交通枢纽进行调查统计,表中列出了某交通路口单位时间内通过的1000辆汽车的车牌尾号记录:
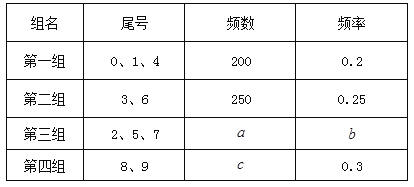
由于某些数据缺失,表中以英文字母作标识.请根据图表提供的信息计算:
(Ⅰ)若采用分层抽样的方法从这1000辆汽车中抽出20辆,了解驾驶员对尾号限行的建议,应分别从一、二、三、四组中各抽取多少辆?
(Ⅱ)以频率代替概率,在此路口随机抽取4辆汽车,奖励汽车用品.用![]() 表示车尾号在第二组的汽车数目,求
表示车尾号在第二组的汽车数目,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中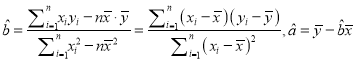 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com