
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论![]() 单调性;
单调性;
(Ⅱ)当![]() 时,设函数
时,设函数![]() 存在两个零点
存在两个零点![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)详见解析;(Ⅱ)证明见解析
【解析】
(Ⅰ)![]() ,分
,分![]() 和
和![]() 两种情况讨论函数的单调性;
两种情况讨论函数的单调性;
(Ⅱ)解法一:由题意可知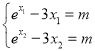 ,两式相减可得
,两式相减可得![]() ,再利用分析法转化为证明要证
,再利用分析法转化为证明要证![]() ,只需证
,只需证![]() ,再通过变形,构造,证明只需证
,再通过变形,构造,证明只需证![]() 即可,
即可,![]() ,构造函数
,构造函数![]() ,利用导数证明
,利用导数证明![]() .
.
解法二:由题意可知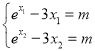 ,再换元令
,再换元令![]() ,即
,即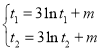 ,两式相减得
,两式相减得![]() ,要证
,要证![]() ,即只需证
,即只需证![]() ,即证
,即证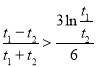 ,再通过变形,构造得到
,再通过变形,构造得到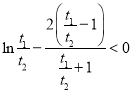 ,
,![]() ,
,![]() ,利用导数证明
,利用导数证明![]() .
.
解:(1)![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() 得
得![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(Ⅱ)解法一:由题意知![]() ,由
,由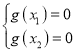 得
得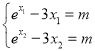 ,
,
两式相减得![]() ,因为
,因为![]() ,故
,故![]() ,
,
要证![]() ,只需证
,只需证![]() ,
,
两边同除以![]() 得
得![]() ,
,
令![]() ,故只需证
,故只需证![]() 即可.
即可.
令![]() ,
,![]() ,
,
令![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,故
,故![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,故原命题得证.
,故原命题得证.
【解法二】
由题意知![]() ,由
,由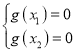 得
得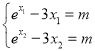 ,
,
令![]() ,即
,即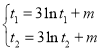 ,两式相减得
,两式相减得![]() ,
,
要证![]() ,即只需证
,即只需证![]() ,即证
,即证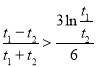 ,即
,即![]() ,即
,即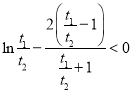 ,
,
令![]() ,只需证
,只需证![]() 即可.
即可.
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,因此原不等式成立.
,因此原不等式成立.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,
,![]() 为
为![]() 的中点,下列说法中正确的是( )
的中点,下列说法中正确的是( )
A.![]() 与
与![]() 所成的角大于
所成的角大于![]()
B.点![]() 到平面
到平面![]() 的距离为
的距离为![]()
C.三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,经过点
,经过点![]() 的直线
的直线![]() 与该双曲线交于
与该双曲线交于![]() 两点.
两点.
(1)若![]() 与
与![]() 轴垂直,且
轴垂直,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() 的横坐标之和为
的横坐标之和为![]() ,证明:
,证明:![]() .
.
(3)设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,该动圆圆心
相切,该动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程
的方程
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,抛物线在点A的切线与
两点,抛物线在点A的切线与![]() 交于点N,求
交于点N,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网正在改变着人们的生活方式,在日常消费中手机支付正逐渐取代现金支付成为人们首选的支付方式. 某学生在暑期社会活动中针对人们生活中的支付方式进行了调查研究. 采用调查问卷的方式对100名18岁以上的成年人进行了研究,发现共有60人以手机支付作为自己的首选支付方式,在这60人中,45岁以下的占![]() ,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
,在仍以现金作为首选支付方式的人中,45岁及以上的有30人.
(1)从以现金作为首选支付方式的40人中,任意选取3人,求这3人至少有1人的年龄低于45岁的概率;
(2)某商家为了鼓励人们使用手机支付,做出以下促销活动:凡是用手机支付的消费者,商品一律打八折. 已知某商品原价50元,以上述调查的支付方式的频率作为消费者购买该商品的支付方式的概率,设销售每件商品的消费者的支付方式都是相互独立的,求销售10件该商品的销售额的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的动点,将矩形
上的动点,将矩形![]() 沿
沿![]() 所在的直线进行随意翻折,在翻折过程中直线
所在的直线进行随意翻折,在翻折过程中直线![]() 与直线
与直线![]() 所成角的范围(包含初始状态)为( )
所成角的范围(包含初始状态)为( )
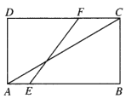
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估![]() 设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 78 | 79 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 93 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的频率):
表示相应事件的频率):
①![]() ;②
;②![]() ;③
;③![]() ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断
,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断![]() 设备的性能等级.
设备的性能等级.
(2)将直径小于等于![]() 的零件或直径大于等于
的零件或直径大于等于![]() 的零件认定为是“次品”,将直径小于等于
的零件认定为是“次品”,将直径小于等于![]() 的零件或直径大于等于
的零件或直径大于等于![]() 的零件认定为是“突变品”,从样本的“次品”中随意抽取2件零件,求“突变品”个数
的零件认定为是“突变品”,从样本的“次品”中随意抽取2件零件,求“突变品”个数![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,该动圆圆心
相切,该动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程
的方程
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点,抛物线在点A的切线与
两点,抛物线在点A的切线与![]() 交于点N,求
交于点N,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com