
【题目】如图所示,在直四棱柱ABCD﹣A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥面A1BD;
(2)求证:MD⊥AC;
(3)试确定点M的位置,使得平面DMC1⊥平面CC1D1D.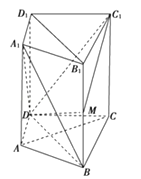
【答案】解:(1)证明:由直四棱柱,得BB1∥DD1且BB1=DD1 , 所以BB1D1D是平行四边形,
所以B1D1∥BD.
而BD平面A1BD,B1D1平面A1BD,
所以B1D1∥平面A1BD.
(2)证明:因为BB1⊥面ABCD,AC面ABCD,所以BB1⊥AC,
又因为BD⊥AC,且BD∩BB1=B,
所以AC⊥面BB1D,
而MD面BB1D,所以MD⊥AC.
(3)当点M为棱BB1的中点时,平面DMC1⊥平面CC1D1D
取DC的中点N,D1C1的中点N1 , 连接NN1交DC1于O,连接OM.
因为N是DC中点,BD=BC,所以BN⊥DC;又因为DC是面ABCD与面DCC1D1的交线,而面ABCD⊥面DCC1D1 ,
所以BN⊥面DCC1D1 .
又可证得,O是NN1的中点,所以BM∥ON且BM=ON,即BMON是平行四边形,所以BN∥OM,所以OM⊥平面CC1D1D,因为OM面DMC1 , 所以平面DMC1⊥平面CC1D1D.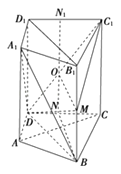
【解析】(1)在平面A1BD内找到和B1D1平行的直线BD即可.利用线线平行来推线面平行.
(2)先利用条件BB1⊥AC和BD⊥AC证得AC⊥面BB1D,再证明MD⊥AC即可.
(3)因为棱BB1上最特殊的点是中点,所以先看中点.取DC的中点N,D1C1的中点N1 , 连接NN1交DC1于O,BN⊥DC面ABCD⊥面DCC1D1 ,
BN⊥面DCC1D1 . 而又可证得BN∥OM,所以可得OM⊥平面CC1D1D平面DMC1⊥平面CC1D1D.
【考点精析】关于本题考查的直线与平面垂直的判定和平面与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.


科目:高中数学 来源: 题型:
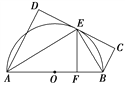
【题目】如图所示,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.
证明:(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在梯形BCDE中,BC∥DE,BA⊥DE,且EA=DA=AB=2CB=2,沿AB将四边形ABCD折起,使得平面ABCD与平面ABE垂直,M为CE的中点.
(1)求证:AM⊥BE;
(2)求三棱锥C﹣BED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() :
: ![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求![]() 的最小值;
的最小值;
(Ⅱ)设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,若点
两点,若点![]() 在第一象限,且
在第一象限,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为(结果保留一位小数.参考数据:![]() ,
,![]() )
)
A.1.3日 B.1.5日
C.2.6日 D.2.8日
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com