
【题目】设m,n(3≤m≤n)是正整数,数列Am:a1 , a2 , …,am , 其中ai(1≤i≤m)是集合{1,2,3,…,n}中互不相同的元素.若数列Am满足:只要存在i,j(1≤i<j≤m)使ai+aj≤n,总存在k(1≤k≤m)有ai+aj=ak , 则称数列Am是“好数列”. (Ⅰ)当m=6,n=100时,
(ⅰ)若数列A6:11,78,x,y,97,90是一个“好数列”,试写出x,y的值,并判断数列:11,78,90,x,97,y是否是一个“好数列”?
(ⅱ)若数列A6:11,78,a,b,c,d是“好数列”,且a<b<c<d,求a,b,c,d共有多少种不同的取值?
(Ⅱ)若数列Am是“好数列”,且m是偶数,证明: ![]() .
.
【答案】解:(Ⅰ)(ⅰ)∵m=6,n=100,数列A6:11,78,x,y,97,90是一个“好数列”, ∴x=89,y=100,或x=100,y=89,
数列:11,78,90,x,97,y也是一个“好数列”.
(ⅱ)由(ⅰ)可知,数列必含89,100两项,
若剩下两项从90,91,…,99中任取,则都符合条件,有 ![]() 种;
种;
若剩下两项从79,80,…,88中任取一个,
则另一项必对应90,91,…,99中的一个,有10种;
若取68≤a≤77,则79≤11+a≤88,90≤22+a≤99,“好数列”必超过6项,不符合;
若取a=67,则11+a=78∈A6 , 另一项可从90,91,…,99中任取一个,有10种;
若取56<a<67,则67<11+a<78,78<22+a<89,“好数列”必超过6项,不符合;
若取a=56,则b=67,符合条件,
若取a<56,则易知“好数列”必超过6项,不符合;
综上,a,b,c,d共有66种不同的取值.
证明:(Ⅱ)由(Ⅰ)易知,一个“好数列”各项任意排列后,还是一个“好数列”.
又“好数列”a1 , a2 , …,am各项互不相同,所以,不妨设a1<a2<…<am .
把数列配对: ![]() ,
,
只要证明每一对和数都不小于n+1即可.
用反证法,假设存在 ![]() ,使aj+am+1﹣j≤n,
,使aj+am+1﹣j≤n,
因为数列单调递增,所以am﹣j+1<a1+am﹣j+1<a2+am﹣j+1<…<aj+am﹣j+1≤n,
又因为“好数列”,故存在1≤k≤m,使得ai+am+1﹣j=ak(1≤i≤j),
显然ak>am+1﹣j , 故k>m+1﹣j,所以ak只有j﹣1个不同取值,而ai+am+1﹣j有j个不同取值,矛盾.
所以, ![]() 每一对和数都不小于n+1,
每一对和数都不小于n+1,
故 ![]() ,即
,即 ![]()
【解析】(Ⅰ)(ⅰ)由“好数列”定义能求出x,y的值,并判断数列:11,78,90,x,97,y是一个“好数列”.(ⅱ)由数列必含89,100两项,若剩下两项从90,91,…,99中任取,有 ![]() 种;若剩下两项从79,80,…,88中任取一个,有10种.由此分类讨论,能求出a,b,c,d共有多少种不同的取值.(Ⅱ)一个“好数列”各项任意排列后,还是一个“好数列”.设a1<a2<…<am . 把数列配对:
种;若剩下两项从79,80,…,88中任取一个,有10种.由此分类讨论,能求出a,b,c,d共有多少种不同的取值.(Ⅱ)一个“好数列”各项任意排列后,还是一个“好数列”.设a1<a2<…<am . 把数列配对: ![]() ,只要证明每一对和数都不小于n+1即可.例用反证法,能证明
,只要证明每一对和数都不小于n+1即可.例用反证法,能证明 ![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=xex(e为自然对数的底数),g(x)=(x+1)2 .
(I)记 ![]() ,讨论函F(x)单调性;
,讨论函F(x)单调性;
(II)令G(x)=af(x)+g(x)(a∈R),若函数G(x)有两个零点.
(i)求参数a的取值范围;
(ii)设x1 , x2是G(x)的两个零点,证明x1+x2+2<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD= ![]() AD,AE⊥PC于点E,EF∥CD,交PD于点F (Ⅰ)证明:平面ADE⊥平面PBC
AD,AE⊥PC于点E,EF∥CD,交PD于点F (Ⅰ)证明:平面ADE⊥平面PBC
(Ⅱ)求二面角D﹣AE﹣F的余弦值.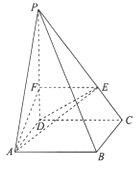
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,点(2,0)在椭圆C上. (Ⅰ)求椭圆C的标准方程;
,点(2,0)在椭圆C上. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点P(1,0)的直线(不与坐标轴垂直)与椭圆交于A、B两点,设点B关于x轴的对称点为B'.直线AB'与x轴的交点Q是否为定点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1 (Ⅰ)求f(x)的最小正周期;
sinxcosx+2cos2x﹣1 (Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在区间[﹣ ![]() ,
, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论: ①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC;⑤平面PBC⊥平面PAC.其中正确命题的序号是 . 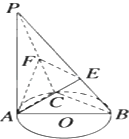
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|2x+a|,a∈R. (Ⅰ)当a=1时,解不等式f(x)≥5;
(Ⅱ)若存在x0满足f(x0)+|x0﹣2|<3,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x+φ),|φ|≤ ![]() ,若f(
,若f( ![]() ﹣x)=﹣f(x),则要得到y=sin2x的图象只需将y=f(x)的图象( )
﹣x)=﹣f(x),则要得到y=sin2x的图象只需将y=f(x)的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com