
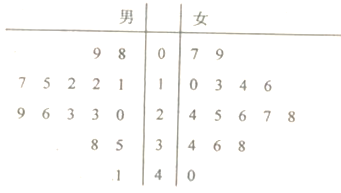
【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查:在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工,对其“每十天累计看手机时间”(单位:小时)进行调查,得到茎叶图如下.所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() ,并且经过
,并且经过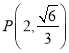 .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“石头、剪刀、布”是个广为流传的游戏,游戏时甲乙双方每次做“石头”“剪刀”“布”三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛,假设甲乙两人都是等可能地做这三种手势.
(1)列举一次比赛时两人做出手势的所有可能情况;
(2)求一次比赛甲取胜的概率,并说明“石头、剪刀、布”这个广为流传的游戏的公平性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,下图是根据刘徽的“割圆术”思想设计的一个程序框图,若运行该程序,则输出的
,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,下图是根据刘徽的“割圆术”思想设计的一个程序框图,若运行该程序,则输出的![]() 的值为( )(参考数据:
的值为( )(参考数据: ![]() ,
, ![]() ,
, ![]() )
)
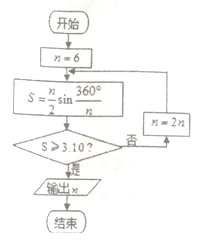
A. 24 B. 30 C. 36 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线![]() 和直线
和直线![]() 交于点
交于点![]() .以
.以![]() 为起点,再从曲线
为起点,再从曲线![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为![]() .若
.若![]() 去九寨沟;若
去九寨沟;若![]() 去泰山;若
去泰山;若![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.

(1)若从![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线![]() 上取点
上取点![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点![]() 在曲线
在曲线![]() 上运动,若点
上运动,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex﹣ax2,曲线y=f(x)在(1,f(1))处的切线方程为y=bx+1.
(1)求a,b的值;
(2)求f(x)在[0,1]上的最大值;
(3)证明:当x>0时,ex+(1﹣e)x﹣xlnx﹣1≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数,且函数
为偶函数,且函数![]() 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com