
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
分析 由题意可得 m=2sinx1+cosx1=2sinx2+cosx2,即 2sinx1-2sinx2=cosx2-cosx1,运用和差化积公式和同角的基本关系式,计算即可得到所求.
解答 解:∵x1,x2是函数 f(x)=2sinx+cosx-m在[0,π]内的两个零点,
即 x1,x2是方程2sinx+cosx=m在[0,π]内的两个解,
∴m=2sinx1+cosx1=2sinx2+cosx2,∴2sinx1-2sinx2=cosx2-cosx1,
∴2×2×cos$\frac{{x}_{1}{+x}_{2}}{2}$ sin$\frac{{x}_{1}{-x}_{2}}{2}$=-2sin$\frac{{x}_{1}{+x}_{2}}{2}$sin$\frac{{x}_{2}{-x}_{1}}{2}$,∴2cos$\frac{{x}_{1}{+x}_{2}}{2}$=sin$\frac{{x}_{1}{+x}_{2}}{2}$,
∴tan$\frac{{x}_{1}{+x}_{2}}{2}$=2,∴sin(x1+x2)=$\frac{2tan(\frac{{x}_{1}{+x}_{2}}{2})}{1{+tan}^{2}\frac{{x}_{1}{+x}_{2}}{2}}$=$\frac{4}{5}$,
故选:C.
点评 本题考查函数方程的转化思想,函数零点问题的解法,考查三角函数的恒等变换,同角基本关系式的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 两条直线都和同一个平面平行,则这两条直线平行 | |
| B. | 两条直线没有公共点,则这两条直线平行 | |
| C. | 两条直线都和第三条直线垂直,则这两条直线平行 | |
| D. | 一条直线和一个平面内所有直线没有公共点,则这条直线和这个平面平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?n∈N,3n<n2+1 | B. | $?{n_0}∈N,{3^{n_0}}<n_0^2+1$ | ||
| C. | ?n∈N,3n≤n2+1 | D. | $?{n_0}∈N,{3^{n_0}}≥n_0^2+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
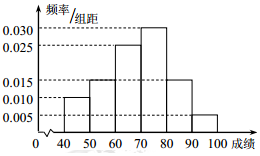 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).| 文科生 | 理科生 | 合计 | |
| 获奖 | 5 | ||
| 不获奖 | |||
| 合计 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-3或4x+3y-15=0 | B. | 4x-3y+15=0 | ||
| C. | 4x+3y-15=0 | D. | x=-3或4x-3y+15=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com